Evolution of this stuff
In post #247, Lee shows us an H&D curve with a bell shaped curve superimposed. If you consider the bell shaped curve to be representing the size frequency curve of the emulsion, then you see the reason behind a typical H&D curve.
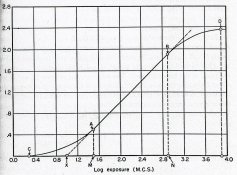
This curve was idealized by H&D in the early days of photography (see my first figure below from Mees, Revised Edition). The best portion of the curve is marked in the figure.
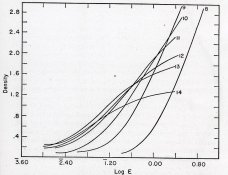
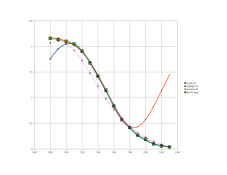
In those days, that type of curve was not easily achieved due to the broad size frequency curves of emulsions made up to about the 50s. These were single run emulsions that produced the family of curves in my second figure below also from Mees. As addition times went up, speed went up but contrast went down. This was due to a broader distribution of grain sizes. Note how bowed the faster curves are. This made measurement and printing on faster films difficult at times.
In the 60s, it became possible to make double run emulsions that gave better speed, sharper toe and through blending, approached the H&D ideal.
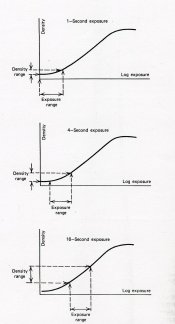
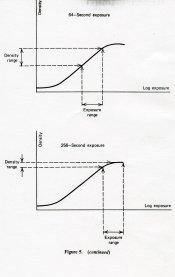
In Haist, Grant shows how to utilize the ideal curve to optimize the Density Range vs the Exposure Range by the simple expedient of insuring that the exposure was off the toe or by giving it a slight overexposure of about 1/3 stop. See the 3rd and 4th figures below.
Unfortunately, in his text, Grant says that you should expose on the toe to compensate for flare, but I believe this was a typographical error, since flare reduces contrast and the toe is low in contrast, the combination would be very bad. I intend to discuss this with Grant in a few weeks while he is visiting Rochester and I'll report back on this.
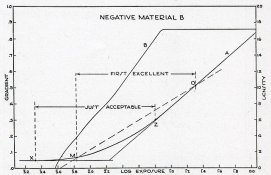
Fortunately, in Mees, in the chapter written by J. L. Tupper, he ran tests in which a relatively straight line (or near ideal) film was used in-camera and in which flare was considered. This data, in the 5th figure, shows the areas of Just Acceptable prints and First Excellent prints. Even though there is overlap, the only portion of the curve (points Z - O) which are Excellent lie vitually completely on the derivative curve shown by Nicholas Linden in his earlier post.
In the final analysis, color films are built with a gamma of about 0.6 - 0.7 and most B&W films are built to that same range or up to .8 so that this flare factor can be compensated for, and they have long straight lines for long latitude, and interestingly enough, the individual color curves of many films reach a gamma of up to 0.8 through interimage effects.
Well, so much for a bit of history of the evolution of this topic.
PE