If weak light shines onto a silver halide grain, it doesn't arrive as continuous flow of light, but as series of distinct photon impacts. While time and location of individual photon impacts can not be predicted, statistical models exist which describe the likelihood of a certain number of photons hitting the crystal. We also know, that each photon impact typically creates one silver atom, and that at least three silver atoms need to be together on one silver halide crystal in order to make it developable. We also know that clusters of two atoms are stable over time, but do not facilitate selective development of the silver halide crystal they are on.
This model makes a lot of assumptions, to the point that it won't predict actual film sensitivity or the full characteristic curve. I will attempt, though, to formulate it in a way that the bottom toe region is properly shown and that differences caused by preflash become apparent.
First of all, let's look at the distribution of light: if we assume silver halide crystals of constant size covering about 30% of the film's area without overlap, and also assume a certain amount of light (power flux density multiplied by exposure time) which creates on average m photon impacts per silver halide crystal, then the probability P(n) of n photons hitting some crystal is calculated as
P(n) = mn / n! * e-m. Absent a preflash the probability of three photons or more hitting a particular crystal is P(n>2) = m
3 / 3! * e
-m + m
4 / 4! * e
-m + m
5 / 5! * e
-m + ....
Because we know that P(0) + P(1) + P(2) + P(n>2) = 1, we can rewrite this ugly sum as P(n>2) = 1 - e
-m * (m
0 / 0! + m
1 / 1! + m
2 / 2!) = 1 - e
-m * (1 + m + m
2 / 2).
Now what happens of we preflash this puppy? Photons coming from preflash are distributed just like those from actual exposure, therefore we can use the same formula, assuming a preflash intensity which creates on average m
p photons per crystal. There are three distinct situations which create a developable silver halide grain:
- Preflash creates three or more photon impacts. Probability P3+ = 1 - e^-mp * (1 + mp + mp^2 / 2).
- Preflash creates exactly two photon impacts, actual exposure creates at least one photon impact. Probability P2 = (mp^2 / 2 * e^-mp) * (1 - e-m).
- Preflash creates zero or one photon impacts, actual exposure creates at least three photon impacts. Probability P01 = (1 + mp) * e^-mp * (1 - e-m * (1 + m + m2 / 2)).
Probability of a silver halide crystal becoming developable after preflash m
p and exposure m is P(m
p, m) = P
3+ + P
2 + P
01. With a decent math program it is trivial to evaluate this formula and draw conclusions about the effectiveness of preflashing at different light levels. Before I throw curves and graphs at you, we need to draw the connection between P(m
p, m) and observed density. Remember, silver halide crystals are tiny, and most densitometers average over lots and lots of grains. If we assume these crystals cover only fraction c of the film area, we can calculate density D = -log
10(1-c * P(m
p, m)). The fraction c will not be all that high, since film consists of crystals of different sizes, but only the largest ones will be affected by the low light intensity we are interested in here. The outcome of this simulation will depend on c, but the general conclusions remain mostly the same. Without giving up any generality, we can continue this model with c=0.3.
One more thing: density is nice, but what we are really after is contrast, which is dD/dm. Also, since m (the average number of photons hitting the crystal) is a linear measure of light intensity, whereas all these graphs thrown around in this thread used log
10(light intensity) as abscissa, we shall follow suit here and plot density D(m
p, log
10(m)) and gradient G(m
p, log
10(m)) = dD(m
p, log
10(m)) / dlog
10(m) for different values of m
p.
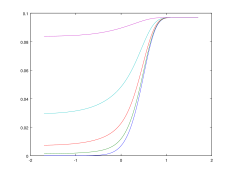
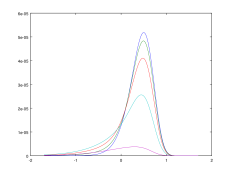
I have run and plotted these formulas with octave, a free matlab clone, resulting curves are attached to this posting. Each graph contains five curves, which represent different values for m
p, starting with m
p = 0 (dark blue), going through m
p = 0.5 (green), m
p = 1.0 (red), m
p = 2.0 (cyan) to m
p = 5 (purple). Remember, that m
p = 3 would be the exposure which gives each grain on average 3 photons, which would be about the lightlevel which creates just barely visible density.
The gradient curves show what we already know from other people's experiences here: preflashing lowers shadow contrast, but provides some contrast in exposure regions where film without preflash gives no contrast at all. This very simplistic model would predict about a half to full stop of additional usable shadow detail.
One more quick note: modern emulsions use two electron sensitization, which creates two silver atoms per photon impact. Such an emulsion should create developable grains with two photons, and this model presented here doesn't cover these emulsions.


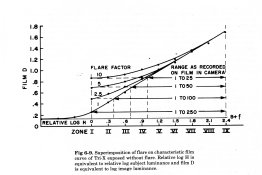


 ) before Athiril (there was a url link here which no longer exists) (see bottom half of his posting).
) before Athiril (there was a url link here which no longer exists) (see bottom half of his posting).