Stephen Benskin
Member
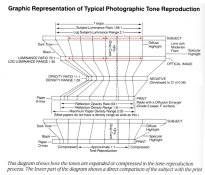
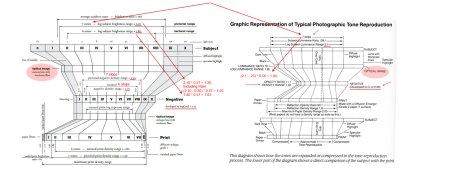
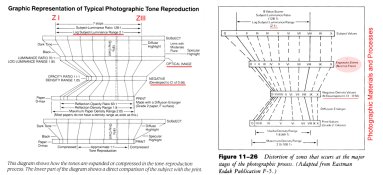
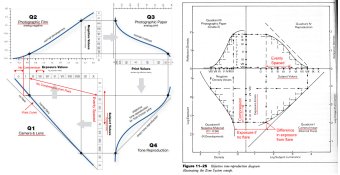
The Kodak Graphic Representation of Typical Photographic Tone Reproduction diagram is fairly well known. Ive always found it to be a excellent illustration of the photographic process, but it contains a lot of information, and sometimes important details can get overlooked. There's a concept hiding in plain sight.
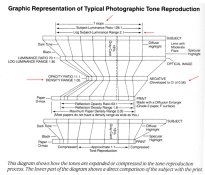
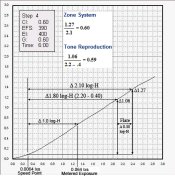
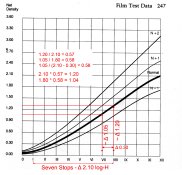
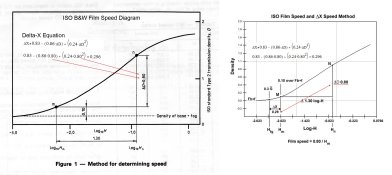
Looking at the diagram, it has a 7 stop range for the subject (log subject luminance range 2.10). And it has a negative density range of 1.05 when the film is developed to a CI of 0.56. According to the equation for slope, Rise/Run, that should be 1.05 / 2.10 = 0.50 and not 0.56. By the looks of things, 0.56 would be over-processing it a bit.

Looking at the diagram, it has a 7 stop range for the subject (log subject luminance range 2.10). And it has a negative density range of 1.05 when the film is developed to a CI of 0.56. According to the equation for slope, Rise/Run, that should be 1.05 / 2.10 = 0.50 and not 0.56. By the looks of things, 0.56 would be over-processing it a bit.



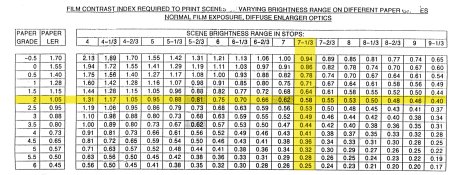
 But lets take a look at the value of the negative density range 1.05. That falls right in the center of the grade 2 paper LER range.
But lets take a look at the value of the negative density range 1.05. That falls right in the center of the grade 2 paper LER range.