Lens hood length - avoiding vignetting

[George]

Eric,
reading you again, I think we misunderstood each other. If you move the shades frame 1cm you should register visually darkening on the gg. In fact the shade is calculated critical - a few mm smaller or longer and it would go on the gg. Usually you see it clearly with 10mm move, but it starts with a few mm already. Therefore I round up the dimension in the length so that in practice it is just a few mm shorter and you're safe from manufacturing imprecision or similar mistakes. Cheers, George.

 

[Helen B]

Eric,

I find this thread interesting because I’ve seen little theoretical treatment of lens hood design using simple, easily measurable design data. Sidney Ray, in Applied Photographic Optics, refers to a few magazine and journal articles but I haven’t been able to get hold of any of them yet.

How much of the hood designed by the formula I gave can you see through the exit pupil? I would not be surprised to find the edges of a rectangular or square hood obscuring a small part of the exit pupil, but the corner of the hood should be very close to the perimeter of the exit pupil, if it is visible at all. I wouldn’t expect a small degree of obscuration to have a noticeable effect on the image.

The derivation of the formula I gave is simple though, unlike George’s method, the distance from the front of the lens hood to the lens should be measured from the edge of the front element, not the front vertex. That only matters if there is a significant curvature to the front element.

Out of interest, what were the given lens and format dimensions, and the calculated hood sizes?


George,

As there is at least one other person interested, we may as well continue in public. I'm also interested to read other people's views on this subject, especially because I know the limitations of the classic, simple method and would like to learn how to refine it. I think that I understand how you do your calculations - I seem to be able to predict the square hood calcs to the nearest 0.1 mm, but I can only predict the rectangular calcs to about 5%. Even in the unlikely event that I have the calculations correct, it is your method and I'll keep my mouth shut.

Here's something that bothers me about using so little information to design a lens hood: You have to make an assumption about the relationship between the diameter of the front element and the field of view. Let's try another example to illustrate this:

Focal length: 52 mm
Front element diameter: 50 mm
Film dimensions: 24 mm x 55 mm
Hood length: 71 mm

What hood dimensions would that result in? I think that George's result would be something like 45.5 mm by 104.5 mm. Is that anywhere near correct? I'm assuming that you can select the hood length with your software, though I suspect that 71 mm might not be the length that you would recommend.

Best,
Helen

 

[Ranger Bob]

So is it wrong for me to use the factory made shades?

 

[resummerfield]

Helen,

I was trying to compute the optimum shade for a Voigtlander Heliar 420mm f4.5 lens, with a lens diameter of 93.2mm, used on an 8x10 camera (245 x 202mm film). The lens will normally be used on axis for studio portraits. George provided several solutions, the optimum shading (his Excellent version) being 113 x 137mm sides extended to 144mm. Using your formula and the same 113 x 137mm sides, it computes to an extension of 112mm. I then made a prototype of each design and installed them on the lens.

Observing the rear element of the lens through the cut-off corners of my ground glass (exit pupil?), I noticed that a small corner of each shade was visible. George’s design obscured around 20% of the exit pupil, while your design, being shorter, obscured maybe 15%. However, neither hood exhibited any darkening of any kind of the ground glass.

Using the shade with George’s computations, I shifted the lens but did not experience total image cut-off on the ground glass until 70mm shift, which really surprised me. However, looking carefully I did notice a slight darkening when shifted about 10-20mm. As another test, I extended the length of the shade with the lens on axis, and did not notice any darkening of the gg until the shade length had reached 175mm. These observations of gg darkening are subjective, of course.

A well designed shade will improve any lens under any conditions, and I routinely use a compendium shade, so I can adjust for lens movements. However, until this exercise, I have not been utilizing the compendium to its full potential. I have always been taught to observe the rear element of the lens through the cut-off corners of my ground glass (exit pupil), and that any distortion of a round aperture indicates vignetting, and should be avoided. Now, thanks to this thread, I’m learning a better way.

I have just exposed a few sheets of a clear north sky, lens at infinity and aperture wide open, and George’s design gives no vignetting. As George said, “The proof is in the pudding.” Now, when using my compendium shade with other lenses, or when using movements, I’m going to try setting the compendium so that a shift of 10mm will not even slightly darken the gg.

 

[Jim Jones]

Eric -- On cameras with the corners cut out on the GG, looking through the opening is probably the most critical way to check for vignetting from both lens barrel and hood. You can detect vignetting this way before it will have a conspicuous effect on photographs. It can be more difficult to evaluate vignetting on the GG. The barrels of many fine lenses vignette at maximum openings. This can slightly affect the reliability of using film for testing the hood. On the other hand, film tests the lens and hood under the conditions where they are actually used. That's what is important, not the theory and math of vignetting.

 

[George]

Helen,
for your latest example, my hood at 71mm length would need 50x114.3mm opening. Once again a different result.
The front lens diameter is indeed very important, as much as the focal length and all the other necessary input values. It must be accounted for in the calculations.
Bob,
it is not wrong - it's just not efficient enough. No lens shade on the market is calculated for your front lens diameter. They are about 70-50 % away from the efficiency of specifically calculated lens hoods, depending on what nonsense you buy. A compendium shade is the most efficient on the market today but again, far away from what you need for your specific film format (they don't imitate it) and the dimension of your lens (they don't count with it either). The problem for marketing the specific lens shades is the fact that you would need literally hundreds of different types for all the combination of lenses and formats. And a universal hood that you could adapt for your combination would not be as elegant as a simple specific example for your lens-format combination. That's the reason that I make my shades for each lens on each film format. They are self supporting and weight next to nothing.
Eric,
I cannot say so much for you shifting tests as that would need to be seen. But you should definitely get vignetting if you use the shade on longer distance than calculated. As I said before, the dimensions are critical (so that you get an efficient hood).

 

[George]

Helen,
one more thing. I saw some of the articles Sidney Ray mentions in his Applied ph. optics. They were not as exhaustive as one would like them to be but showed the importance of a good lens hood. It was one of the reasons that I dived for it. After all, as you noticed, it's a fascinating geometric subject with important practical consequencies.

 

[Helen B]

Helen,
for your latest example, my hood at 71mm length would need 50x114.3mm opening. Once again a different result.
The front lens diameter is indeed very important, as much as the focal length and all the other necessary input values. It must be accounted for in the calculations.
...

The thing is that if you use the diameter of the front element, you have to make an assumption about the relationship between the extremities of the field of view and the diameter of the front element - ie you assume that the image circle of the lens is just adequate to cover the format. That assumption cannot be made if the lens is being used for a format significantly smaller than the lens will cover. The 52 mm f/l example I gave is a good example. In the original case the lens (a Zeiss Distagon) was being used for a full-frame (55 mm x 55 mm) image. The lens hood was calculated to be 71 mm long, with sides of 88 mm. The second calculation was for a central crop from that frame, 24 mm high and 55 mm wide. The lens hood, at the same distance from the front vertex, is now calculated to be 114 mm wide. Why isn't it still 88 mm wide? Because the assumption about the front element is not valid. This applies to both George's method and the 'classic' method I gave.

It would be better to use the location and size of the entrance pupil, if it is known or if it can be measured. You replace the front element diameter with the entrance pupil diameter, and the distance to the front of the lens hood is the distance from the entrance pupil instead of from the front element. The formulae would be different. I'll draw it all out and append the drawing as soon as I have time, and re-state the simple formulae and assumptions.

An aside: I'm still puzzled about why I can predict George's results for square format to better than one millimetre, but can only predict his non-square format measurements to within about 10%, as in this case.

Best,
Helen

 

[George]

Helen,
sorry to say it, but your assumptions you put into my mind or my method are completely inexistant and therefore wrong.I think you're a little bit lost in it. Unlike what you suppose, I calculated hoods for lenses with more than 600mm image circle while using from it only 6x9 format! Not at all according to your assumptions about my method. And I have many hoods for lenses where the used film format is much smaller than the image circle, simply because I use these lenses for smaller formats too. All these hoods I have, work perfectly and are critical in their dimensions. Enough said. Cheers, George

 

[George]

Helen,
after some more thoughts about it (but I'm not able to give it more time as I have urgent tasks now) - the diameter of the front element is related to the relations in front of the lens, not behind. Cheers, George.

 

[George]

And one more for your thoughts, Helen,
- it is not as easy as to say -the format is half, then the shade will be halfed too for the same length of the hood (square or not). As I said already several times, the hood changes its dimension in a non linear way when you change its length. Nor can you assume that if one of the film format's side is constant that it would mean one of the hood side is constant too. The relations are more complicated than that (and in fact in some way also easier...) Anyway... George

 

[George]

... In the original case the lens (a Zeiss Distagon) was being used for a full-frame (55 mm x 55 mm) image. The lens hood was calculated to be 71 mm long, with sides of 88 mm. The second calculation was for a central crop from that frame, 24 mm high and 55 mm wide. The lens hood, at the same distance from the front vertex, is now calculated to be 114 mm wide. Why isn't it still 88 mm wide? Because the assumption about the front element is not valid. Best,
Helen

It's for an entirely different reason than you think... and a very simple one! Nothing to do with your assumption (which is not mine). Heck, I have to shut up now... George

 

[Helen B]

And one more for your thoughts, Helen,
- it is not as easy as to say -the format is half, then the shade will be halfed too for the same length of the hood (square or not). As I said already several times, the hood changes its dimension in a non linear way when you change its length. Nor can you assume that if one of the film format's side is constant that it would mean one of the hood side is constant too. The relations are more complicated than that (and in fact in some way also easier...) Anyway... George

George,

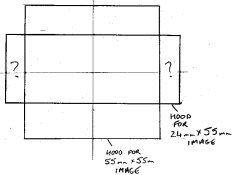
If an opening of 88 mm x 88mm is adequate to pass all the image-forming rays heading towards a 55 mm x 55 mm image, why do enlargements (marked with a question mark in the sketch) need to be made to the opening to pass all the rays heading towards a smaller image? What rays pass through these enlargements, and why weren’t they necessary for the larger image format? I find those questions difficult to answer, and I would appreciate your assistance.

Your assumptions: I wonder whether the relationship between the film format and the diameter of the front element is an implicit assumption, if it is not an explicit one. The results that you have given in this thread appear to suggest that it is. The diameter of the front element need not appear in the image-side calculations for the relationship to exist.

If the front element is relatively close to the entrance pupil, it won’t make a lot of difference which one is used for the calculations.

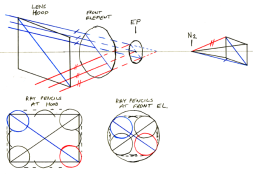
Here is the reasoning behind the ‘classic’ simple method. I would welcome any comments, especially critical ones. It is a lot easier to draw out step by step than it is to explain, but I’ll give it a go.

Purpose: To design a lens hood given only the film format, lens focal length and the diameter of the front element of the lens.

Note: This amount of information is inadequate for designing an optimal lens hood, but it can be used for an approximate design.

Image-side calculation.
Construct a triangle with a base equal to the diagonal of the film format and height equal to the lens focal length. This represents the diagonal field of view of the lens/film, and the apex lies at the rear (second) nodal point of the lens.

That is the full extent of the image-side calculation.

Object-side calculation.
Draw the lens axis, and place the centre of the entrance pupil at some point on the axis. You don’t need to know where the entrance pupil is.
Construct a triangle on the axis similar to the image-side one (in practice, this is the same triangle, extended as necessary). This represents the two rays that will pass through the centre of the entrance pupil, then arrive at the corners of the image.

When the lens is focused at infinity these central rays will be surrounded by parallel rays from the same object point that will be focused at the corners of the image. The ray bundles will be bounded by the entrance pupil. (There may also be other restrictions, but these will be ignored for the purposes of this approximate calculation, because they are unknown). Because the peripheral rays in the ray bundles are parallel to the central rays, the angle between the central rays equals the angle between the peripheral rays, and the same two lines can be used to describe the extremities of the ray bundles. The entrance pupil is now at some unknown point along the axis, away from the apex of the triangle.

Because the location of the entrance pupil is unknown, we will have to make the assumption that the rays that graze the edge of the entrance pupil also graze the edge of the front element. This is not necessarily true, but the closer the front element is to the entrance pupil, the less error will be introduced. If the position and diameter of the entrance pupil is known, it can be used in place of the front element, if it is more restricting than the front element. (This can apply if a lens is used for a format smaller than the image circle of the lens, and there is a significant distance between the entrance pupil and the front element).

The diagonal of the lens hood at any point in front of the front element can now be measured or calculated by simple geometry. It need not be done by trigonometry.

The sides of a rectangular or square hood can now be calculated from the diagonal. Note that the bundle of rays heading towards the film will have rounded corners, and squaring those off from the diagonal results in a square or rectangle that is slightly smaller than the ray bundle, but this does not normally matter in practice. The closer the hood is to the entrance pupil, and the wider the aperture, the more this squaring-off will obstruct the peripheral rays.

It is quite possible for a rectangular hood to have a side smaller than the diameter of the front element. In some cases both sides can be shorter than the diameter. If the entrance pupil is used in the calculation, no side of the hood should ever be shorter than the diameter of the entrance pupil.

Best,
Helen

 

[George]

Helen,
obviously, I don't want to explain my algorithms - neither in small details nor in the buff -for the reasons already mentioned. I'm not interested in telling you exactly where you are mistaken or not precise in your assumptions either - for the same reason. To describe these things verbally is - at least for me - simply exhausting. All I was doing were just giving you hints - doing so in the smallest details would be the same like revealing all the programme...
The problem you touch in your first question is interesting enough to be thought over - the answer is as logic as it is surprising...
If ever you come with some other way of calculating the hoods I'm already sure of this: if your hood dimensions are smaller than mine, you will get vignetting. If they are bigger, you will get a hood with much smaller efficiency. If they are the same - nothing new for me then.
Cheers, George

 

[Helen B]

This diagram might help to clarify what I understand to be the reasoning behind the classic method.

Notes
The projection of the entrance pupil forwards assumes that there is no barrelling effect – for many lenses this will not be true because the entrance pupil will be partially obscured in the corners of the frame. The effect of this could be shown in another diagram – which I could draw later. Cutoff caused by the rear group does not affect the hood calculation because it is on the wrong side of the ray pencils.

The slight cut-off associated with squaring off the diagonal is shown. If there is any interest, I’ll draw a second diagram to show that if the front element causes cut-off, the loss caused by squaring the diagonal increases a little. Thas would be a case where using the entrance pupil for the calculations may be preferable – or maybe a compromise between the entrance pupil and the front element.

The entrance pupil does not physically exist: it is the virtual image of the iris as seen from the front of the lens.

As the diagram shows, it is a three-dimensional problem that can be recast as a two-dimensional problem by choosing the plane through the film diagonal and the optical axis (drawn in blue and red).

While Googling for enlightenment on this subject, I came across an Excel spreadsheet by J C O’Connell, hoodcalc.xls, also available as hoodcalc.zip. Though it uses trigonometry, it is exactly the same calculation as the one I outlined – the trig is unnecessary, but it isn’t a burden in an Excel spreadsheet. The equation I gave also happens to be given by Cox in Photographic Optics, as I discovered, but he gives no explanation of it. He gives two other versions of the equation, both of which appear to be incorrect. That makes me think that he hadn't thought through the problem in three dimensions.

Best,
Helen

 

[Helen B]

I thought that it might be worth looking at another, even simpler, way of calculating lens hood dimensions: a rule of thumb used in large format photography. The idea is that a compendium lens hood should mirror the camera bellows and film aperture – ie the aperture in the hood should be the same size as the film format, and the distance from the lens should equal the bellows draw. The optical axis should be maintained (ie the hood movements should correspond with the camera movements).

At first sight that may seem to be too severe, so that it would result in cutoff. For a simple single element lens, it would result in a 50% cutoff of the ray pencils heading towards the periphery of the frame.

In practice, it often works out quite well. Why?

1) Some cutoff of the peripheral rays is permissible, in fact the best lens hoods do cause some cutoff (seen as slight obstruction of the exit pupil when viewed from the back of the camera).

2) The degree of cutoff diminishes rapidly for ray pencils that are not heading towards the periphery of the frame. The smaller the f-stop, the more rapid the decrease in cutoff. This is a large format rule, and large format cameras are often used at small apertures.

3) If the nominal format is used for making the hood aperture, some imagined cutoff of the nominal film format will be outside the actual film frame – so it will not be cutoff.

4) Many lenses will have some degree of barreling anyway (the front group causes some obstruction of oblique rays). This will not be true when the film frame is well within the image circle of the lens.

5) As the lens is focused closer, the field of view decreases. The rule of thumb follows that property.

6) Most lenses used in LF are symmetrical. When the rule is applied to telephotos, which have less bellows draw than a symmetrical lens, it would lead to hoods that are too short – ie the error takes the hood out of the field of view. Retrofocus lenses, which would result in hoods that were too long, are very rare in LF.

George has given some dimensions in this thread that are very similar to those that would be produced by the rule of thumb:

"1) 55mm lens: length of the shade 54mm, sides AxB = 129.1 x 101.1 mm.
2) 80mm lens; length 80mm, sides AxB = 129.1 x101.1 mm."

This is for 4x5, for which the actual frame is 94 mm x 120 mm. George’s hood dimensions are very close to 4 inches by 5 inches, and the hood length is close, or equal to the lens focal length. In practice both these hoods are slightly too small for 94 mm x 120 mm when the lenses are used wide open and focused on infinity but they would be usable when the lens was stopped down, focused on a closer object (this effect is particularly relevant in practice for a hood made to fixed dimensions), or with a small adjustment to a compendium hood.

For formats other than LF the rule of thumb would need to be applied with an understanding of its limitations. The saving factor is that often the front part of the lens itself may cause some cutoff of the peripheral rays, especially with wide aperture lenses.

Best,
Helen

 

[DBP]

Wow. I wasn't sure when I started this thread that I would get any answers. For what it is worth, the lens hood arrived last week and does not vignet noticeably on ground glass placed at the film plane. Now I just need to scuff it up so it matches the very battered lens barrel.

 

[George]

To those interested...
Please beware of the fact that I personally take a great distance from the above expressed assumptions. In the calculations of a good lens hood the lens diameter is a very important measure (you know by yourself that a lens with a great lens diameter is more prone to the flare than a lens with a small front diameter.) If for ex. the ex.1) seems to be somehow close to a nominal 4x5 film format then know that with a different front lens diameter the hood dimension is already changed. It doesn't follow any easy rule. Also, none of my calculated lens hood ever caused any vignetting - they work with the widest apertures with no problems at all. Just so that you know better. George

 

[orto]

A fascinating reading, George. I admire your idea of calculating in a scientific and precise way lens hood dimensions. I think it's completely unknown to anybody else, at least I've never found anybody who would do it. If you read this message, can you give me a PM? I would like to know more about your knowledge. Thank you very much for any answer from you.

 

[Q.G.]

You cannot be scientific about calculating the desired length for a lens hood without also knowing the particular barrel a particular lens goes in.
It's different for every different lens - barrel combination.

 

[orto]

Can you explain what do you mean by "knowing the barrel" of a lens? Thanks.

 

[Q.G.]

Can you explain what do you mean by "knowing the barrel" of a lens? Thanks.

You need to know, for instance, how deep the front lens is recessed inside the barrel, i.e. the distance between the front lens and the mount the hood is to go on.

 

[orto]

You need to know, for instance, how deep the front lens is recessed inside the barrel, i.e. the distance between the front lens and the mount the hood is to go on.

I think George has taken care of it in an excellent way - he measures the length of the hood from the lens vertex. In this way he calculates the needed length and the hood is constructed accordingly. That's how I understood his posts.
Still waiting for your reply, George. Thank you.

 

[orto]

I think George has taken care of it in an excellent way - he measures the length of the hood from the lens vertex. In this way he calculates the needed length and the hood is constructed accordingly. That's how I understood his posts.
Still waiting for your reply, George. Thank you.

Thanks to an Apug member I entered in contact with George. He laughed at the mention of measuring the lens hood length from a lens barrel as suggested in a post. He confirmed my understanding of his method (the length is calculated from the lens vertex). He's now on a foreign travel and will come back to me with more to say - it seems that he gets questions about the lens hood calculation from other people on Apug and helps them but he himself is not a member.

 

[Q.G.]

He laughed at the mention of measuring the lens hood length from a lens barrel as suggested in a post.

Must be because of the way it was presented to him.
Unless you mount a lens hood on the very lens vertex itself, the distance between the vertex and the mount where you can mount the thing must be taken into account, subtracted rom the hood length.
And that distance is different for different lenses. Is a feature of the barrel.

I know that some people put a lot of trust in theoretical considerations.
But unless you want to remain stuck in a theoretical world, it pays to be practical too.