Like shortening flash-duration at an electronic flashlight. In practice already the delivered electrical energy is huge, though only for an extreme short time. Reducing duration time to infinitively small values would make the spent energy infintively large.
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
inverse ssquare law
-
A
- Thread starter RalphLambrecht
- Start date
Recent Classifieds
-
For Sale Voigtländer Skopar 300mm f/4.5 (Germany, 1930) _ brass lens
- Started by Manual Camera
-
Want to Buy WTB: Bulk quantities of 35mm PAPER slide mounts
- Started by FieldPhoto
-
For Sale Custom Hand Held 4x5 Camera - Sinar Handy w/ 65mm f/8 Super Angulon
- Started by pdccamerqs
-
For Sale Schneider-Kreuznach Super Angulon 5.6/65mm
- Started by pdccamerqs
-
For Sale FotodioX Pro Right Angle View Finder Hood for 4x5 Sinar Camera
- Started by pdccamerqs
Forum statistics
Maris
Member
If you want another confounding factor think on this. The light intensity at any point in space away from a point light source is zero. A point in space has zero area so no photons can pass through it. And yet an illuminated surface consisting notionally of uncountable points with no spaces between them does intercept photons.
fretlessdavis
Member
If you want another confounding factor think on this. The light intensity at any point in space away from a point light source is zero. A point in space has zero area so no photons can pass through it. And yet an illuminated surface consisting notionally of uncountable points with no spaces between them does intercept photons.
It's not a series of points, it's called a plane. Planes have area, points don't. Points are points in space, and have no volume. Planes are a surface that occupies space....
fretlessdavis
Member
Like shortening flash-duration at an electronic flashlight. In practice already the delivered electrical energy is huge, though only for an extreme short time. Reducing duration time to infinitively small values would make the spent energy infintively large.
This is not true.
Shortening a flash-duration would not increase the instantaneous power output of the flash, it would stay the same. To attain the same overall light output hitting the subject, you'd have to increase the instantaneous power output of the flash.
StoneNYC
Member
In out, PM me if you want me to ask my dad anything else...
RPC
Member
- Joined
- Sep 7, 2006
- Messages
- 1,630
- Format
- Multi Format
As the distance approaches zero, the intensity asymptotically approaches infinity. You can never reach zero distance.
Then how does something "approach" zero or infinity? No matter how small something gets, it is always infinitely far away from zero, and now matter how large, it is always infinitely far away from infinity.
Chan Tran
Subscriber
I think if the light source is a true point source that is a point with no dimension then it's possible to have infinite intensity
Prof_Pixel
Member
Then how does something "approach" zero or infinity? No matter how small something gets, it is always infinitely far away from zero, and now matter how large, it is always infinitely far away from infinity.
I take it you've never studied calculus? It includes a study of limits (as in the limit when something approaches zero or infinity).
RalphLambrecht
Subscriber
I think if the light source is a true point source that is a point with no dimension then it's possible to have infinite intensity
that was my point ,hence the doubt about the equation

Bill Burk
Subscriber
- Joined
- Feb 9, 2010
- Messages
- 9,373
- Format
- 4x5 Format
I was going to say maybe the limit was a half-inch. But looking at the kinds of devices that you can setup to take advantage of inverse square law, I could imagine a "grease spot photometer" could be invented to fit within a rangefinder of a camera, and there's no reason this device couldn't be a quarter-inch overall and still be effective.
Curt
Member
As the distance approaches zero, the intensity asymptotically approaches infinity. You can never reach zero distance.
Yes.
Curt
Member
I take it you've never studied calculus? It includes a study of limits (as in the limit when something approaches zero or infinity).
Exactly!
This is not true.
Shortening a flash-duration would not increase the instantaneous power output of the flash, it would stay the same. To attain the same overall light output hitting the subject, you'd have to increase the instantaneous power output of the flash.
You are right in practiice: control of flash duration is actually used for switching light outpu. I was thinking of an energy/time couple where one could control one element, but the spent work, the quotient, would be constant.
This is not the case. But there also is no W/sec in reality. As no flash extends to a second. Still we use this analogon, as if the flashlight always does the same electrical work.
RPC
Member
- Joined
- Sep 7, 2006
- Messages
- 1,630
- Format
- Multi Format
I take it you've never studied calculus? It includes a study of limits (as in the limit when something approaches zero or infinity).
I just don't think the phrasing is very meaningful. For example I think something like "increases without bound" might be a better way to phrase it than "approaches infinity".
Ed Bray
Member
To be frank, whilst the theory can be fascinating, it has no practical use in photography once you get less than a useable distance from the point source, especially when the source no longer can be classed as a point source.
Who is actually making images at less than 3" from a source using something that equates to a point source, a single LED perhaps? To use the inverse square law practically you need to be able to measure the light at one point to be able to use the ISL to calculate the light strength for another, at very close distances this becomes extremely impractical.
Nowadays if someone is using d*****l they just chimp the image until they get it as they want it, if small point sources of light are being used to highlight parts of an image, the image was also chimped in the pre-d*****l days with the use of a polaroid.
Who is actually making images at less than 3" from a source using something that equates to a point source, a single LED perhaps? To use the inverse square law practically you need to be able to measure the light at one point to be able to use the ISL to calculate the light strength for another, at very close distances this becomes extremely impractical.
Nowadays if someone is using d*****l they just chimp the image until they get it as they want it, if small point sources of light are being used to highlight parts of an image, the image was also chimped in the pre-d*****l days with the use of a polaroid.
Chan Tran
Subscriber
that was my point ,hence the doubt about the equation
but then there is no true point light source.
RalphLambrecht
Subscriber
but then there is no true point light source.
how does that effect the validity of the law?:confused:
RalphLambrecht
Subscriber
To be frank, whilst the theory can be fascinating, it has no practical use in photography once you get less than a useable distance from the point source, especially when the source no longer can be classed as a point source.
Who is actually making images at less than 3" from a source using something that equates to a point source, a single LED perhaps? To use the inverse square law practically you need to be able to measure the light at one point to be able to use the ISL to calculate the light strength for another, at very close distances this becomes extremely impractical.
macro/micro photography
 moving a flash gun extremely close to max light intensity,being aware of light loss dou to bellows extension
moving a flash gun extremely close to max light intensity,being aware of light loss dou to bellows extensionblockend
Member
Light is weird stuff. It can be wave or particle, depending on whether someone is observing it (see double slit experiment). That's why photography is really a magical-alchemical process, even while we imagine it's a practical-mechanical one. Summoning the muse is much cheaper and infinitely more effective than throwing money at new gear.
michaelbsc
Member
how does that effect the validity of the law?:confused:
From http://www.nukeworker.com/study/hp/neu/Part_2_Radiation_Protection/RP-4_Radiation_Protection.pdf
"Line and plane sources can appear as point sources if the distance from source to
measurement point is great enough. There is a rule of thumb used when considering a
source a point source. A source will exhibit the characteristics of a point source if the
measurement point to source distance is greater than three times the largest dimension of
the source."
Radiation, whether it's visible light falling on a photography subject or gamma radiation dosing a worker works the same.
As we get closer to the light source, we eventually get to the point that it no longer can be approximated by using rules of a point source.
If it were - in fact - a "true point source" then if you crossed into the singularity it would be infinite, maybe. The math breaks down in stuff like that.
So, the formula isn't wrong, nor is the theory. What's wrong is the assumption that the illumination source is a point. But the math to calculate it, vs the math to approximate it, is orders of magnitude different.
A plane source, like the surface of the bulb, will have a constant dose (or in our case illumination) regardless of the distance so long as we stay within in the 3x parameter. For example, if we are 2cm away from a 5cm bulb radiating surface, and we move to 4cm we will not effectively change the illumination of the subject. If we move to 10cm we will not "effectively" change the illumination. If we move to 15cm we will not effectively change the illumination. But if we move to 30cm we will get the inverse square illumination.
Again, these are rules of thumb that plenty darn good enough approximations to live with. While the actual mathematical calculation isn't difficult in principle, it is devilishly difficult to compute in a practical sense.
That is a good explanation, Michael.
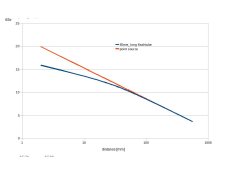
I am not doing macro but yesterday I made a graph based on my earler post.
The vertical scale is 'relative EV" to indicate change in camera settings for example f/ (by taking log-base2 of the change in luminance [cd/m^2]
Graph is for a 65mm long flash tube.
It also shows that after the distance is further than 2~ 3 times the length of the flash tube, the Gauss Law (inverse square)
is quite accurate.
Closer than that, the EV settings do not change so much.
I am not doing macro but yesterday I made a graph based on my earler post.
The vertical scale is 'relative EV" to indicate change in camera settings for example f/ (by taking log-base2 of the change in luminance [cd/m^2]
Graph is for a 65mm long flash tube.
It also shows that after the distance is further than 2~ 3 times the length of the flash tube, the Gauss Law (inverse square)
is quite accurate.
Closer than that, the EV settings do not change so much.
Attachments
michaelbsc
Member
That is a good explanation, Michael.
I am not doing macro but yesterday I made a graph based on my earler post.
American taxpayer money at work. I spent almost 24 months in technical schools in the US Navy learning that, plus a million other things.
| Photrio.com contains affiliate links to products. We may receive a commission for purchases made through these links. To read our full affiliate disclosure statement please click Here. |
PHOTRIO PARTNERS EQUALLY FUNDING OUR COMMUNITY:  |