In response to those who wish to be apprised of my C-41 methodology

[mtjade2007]

I understand ........ and that the A and B concentrates are separate for good reasons (notably interactions between sulfite and hydroxylamine IIRC). Hence, pre-mixing A and B and storing them for extended periods of time will affect the nature of the developer, influencing overall activity and/or color balance.

I am not a chemistry person so I can only report my experience here at 2 cents worth. I did pre-mix part A, B and water at 4 times concentration (2.5 liters instead of 10 liters from my 10 liter replenisher kit) and kept it for more than a year without any detectable degradation. I can understand now there can be good reasons Kodak have them in separate bottles. But to me nothing bad happened. I also understand that part C contains more than just CD-4. But for some reason I used 5 grams of CD-4 powder per liter in place of the gone bad part C. There wasn't any detectable color shift or anything else bad I could tell. I once asked PE if I needed to add anything in addition to just CD-4. He said if nothing bad happened I could just do it. There wasn't really a satisfactory answer from him. I have always wondered if I really need additional stuff so that my replacement part C is more complete or accurate.

 

[mtjade2007]

I have used a method similar to mtjade2007 except I mix parts A and B separately and keep them separate until use. (I received a large amount of C-41 developer replenisher from the lab I worked at when they quit processing film years ago.) When mixing I add 5 grams of CD-4 (the original liquid went bad long ago) and the proper amount of starter, then just adjust the pH to about 10.1. This way I have used the lab chemistry over a period of years with no apparent degradation. Some of it was completely mixed years ago, stored in full glass bottles and still seems to work well after adjusting the pH.

Great idea to pre-mix part A and B in separate containers to keep them long term. I never thought of that. That's the way to go. I never needed to adjust the PH after adding CD-4. I believe the part A and B have the PH adjusted already. I got the impression that PE said that before. Anyway, I have had a PH meter and some probes for years. But since I am not a chemistry person I never really figured out how to use it. I was troubled by the requirement of calibration before making any PH measurement. I figured that I could not calibrate it correctly based on my very limited knowledge of the instrument. So my PH meter has gone unused for decades.

 

[RPC]

The pH may be a bit high since there is no SO2 or bisulfite/metabisulfite in the mix, and I found that to be often be the case and so adjust it. It may not make a lot of difference, your negatives may be fine without doing it, in fact it may add a bit of contrast and appeal to your pics!

 

[Rudeofus]

I wonder, if Kodak indeed protected CD3 with bisulfite, why they'd choose the probably more complex solution of saturated SO2 for C41 concentrate.

Do you know for sure, that Kodak uses saturated SO2 solution? The amount of Sodium Metabisulfate in Kodak's CD part concentrate is quite low.

I did pre-mix part A, B and water at 4 times concentration (2.5 liters instead of 10 liters from my 10 liter replenisher kit) and kept it for more than a year without any detectable degradation. I can understand now there can be good reasons Kodak have them in separate bottles. But to me nothing bad happened. I also understand that part C contains more than just CD-4. But for some reason I used 5 grams of CD-4 powder per liter in place of the gone bad part C. There wasn't any detectable color shift or anything else bad I could tell.

I have no concentrate formulas, but from what I have seen in MSDS, the three parts of C-41 CD concentrate are divided into CD-4 plus traces of Bisulfite/SO2 (part C), Hydroxylamine Sulfate (part B) and The Rest (part A). At higher salt concentrations less air enters the liquid, which means two things: less CO2 lowering pH of the alkali part, and less Oxygen destroys reducing agents (HAS and CD-4). If the HAS is gone, the color developer show comparable results but will have much reduced working solution life. I would therefore not predilute any concentrate part if shelf life was a concern.

 

[koraks]

Do you know for sure, that Kodak uses saturated SO2 solution?

Nope, I don't! Come to think of it, probably not.
I may run the numbers on the bisulfite addition and do a small-scale test.
I did make a tiny amount of CD4 solution in vinegar (ca 7% acetic acid), but that shows significant oxidation within a day, so that route doesn't seem to work. Bisulfite sounds more promising.

 

[RPC]

I have no concentrate formulas, but from what I have seen in MSDS, the three parts of C-41 CD concentrate are divided into CD-4 plus traces of Bisulfite/SO2 (part C), Hydroxylamine Sulfate (part B) and The Rest (part A). At higher salt concentrations less air enters the liquid, which means two things: less CO2 lowering pH of the alkali part, and less Oxygen destroys reducing agents (HAS and CD-4). If the HAS is gone, the color developer show comparable results but will have much reduced working solution life. I would therefore not predilute any concentrate part if shelf life was a concern.

So what if one was to use pre-diluted and stored part A, mixed with 5 grams CD-4 (and starter if appropriate), scrapped the part B altogether, adjusted the pH, and used the developer up in a timely fashion. Do you think one could expect reasonably normal results? I'm thinking of trying that.

 

[Rudeofus]

So what if one was to use pre-diluted and stored part A, mixed with 5 grams CD-4 (and starter if appropriate), scrapped the part B altogether, adjusted the pH, and used the developer up in a timely fashion. Do you think one could expect reasonably normal results? I'm thinking of trying that.

There's a lot of focus on aerial Oxygen, but let's not forget Carbon Dioxide! Carbon Dioxide will happily dissolve in alkaline solution and lower pH. This will not be immediately apparent, since color developers are well buffered, but in the long run this could become a problem. And honestly: is there any credible reason to predilute the concentrate?

About the other concentrates: I guess one could replace concentrate part C with a suitable amount of CD-4. Not sure whether one can safely omit the HAS. HAS is used to protect CD-4 from aerial oxidation, but it's also a B&W developer, which means it will reduce dye formation. Its effect has been accounted for in C-41 film stock, so leaving out the HAS could lead to color shifts. Since HAS is easy to obtain from the same places which sell CD-4, I recommend adding it to C-41 CD unless there are strong reasons against using it, or at least conclusive tests confirming that it has no pictorial effect.

 

[RPC]

My thinking is I would mix a large amount of part A at a proper dilution with starter added, decant it into about 1 liter bottles and store these until use, then mixing time for making developer would be reduced. All I would have to do is add CD-4 (which could be pre-measured) and perhaps a little water to make 1 liter. The pH would then be adjusted just before use, compensting for CO2 and missing HAS. Alternately, I could pour out the liter of part A pre-mix from a large container into a 1 liter bottle just before use.

The only issue then would be the missing HAS and I guess I will just have to try it to see what image and storage problems it may cause .

 

[Rudeofus]

How about this: you keep the concentrate A as it is (and enjoy its incredible shelf life), and when you mix C-41 CD, you first prepare some amount of water with the CD-4, then add the part A concentrate to make the amount you want. If you can handle some process variations and use the CD fresh anyway, there's a good chance, that the HAS won't be missing. Or you prepare it in little bags for 2 g/l in working solution.

But let's be honest: souping C-41 film takes well over 20 minutes if you also count the washing, and preparation of everything from spooling the film all the way to cleaning up afterwards takes even more time. Given all that: are you really sure, that premixing C-41 CD is such a big time saver?

 

[RPC]

I guess I will ponder the different methods to decide which will work the best for me.

If eliminating the HAS works well I might even try experimenting with home-brew C-41 developer formulas without HAS.

 

[Rudeofus]

Any specific reason for avoiding HAS ?

 

[koraks]

Any specific reason for avoiding HAS ?

Good question. Personally, while I generally use C41 dev one shot or at least within a day or 3, I always add HAS anyway. Why risk inexplicable issues by leaving it out? (Note: I already take enough risks by DYI-ing my C41 developer as it is...)
Of course, one could systematically test with and without HAS and comparing test strips developed immediately, after 12 hours, 24 hours, 48 hours, 72 hours etc., but frankly, I personally am way too lazy for that. Besides, why fix what ain't broken...

 

[RPC]

For home-brew, it is just another ingredient to have to buy, store and mix. Why use it if it is not needed for my purposes? After I would mix a liter of developer I would use it up quickly so the only real issue would be image quality. I have a densitometer so am able to run tests on curve shapes and other factors, which I do in all my C-41 work.

 

[koraks]

If by 'quickly', you mean within about 48 hours, then I can see the sense in leaving it out. I think the influence of omitting HAS is something like a few percent less overall density per 24 hours; effect on color balance unknown.

 

[RPC]

Actually I think it would be quite a bit more than 48 hours due to the sulfite in the formulas, if stored in full, glass jars.

 

[koraks]

There's by far not enough sulfite in c41 to be effective as an antioxidant.

 

[RPC]

C-41 developer was designed for labs and as such needs a lot of oxidation protection for the aerial exposure it will continually experience in a processing machine even with replenishment. HAS is used for this as too much sulfite interferes more with dye formation. But for home use aerial oxidation is not as much of a concern if stored correctly and used one-shot, especially in a small inversion tank as I use. Some of the formulas I have tried have 3-4 grams of sulfite which is a safe level and I am confidant this will protect the developer from the air dissolved in the solution for quite some time. If the developer is stored in glass and sealed tightly it will be protected from outside air. But that will be the point of all my tests--to see what actually happens.

 

[Rudeofus]

Please note, that HAS also develops exposed silver halide, which means there will be exposed and developable silver halide, which will not form color dyes because of it. Since the designers of C-41 film know this, they design their film accordingly. If you leave out HAS, there may be too much dye formation in some color layers and in certain density ranges. This is relevant from the first minute on, and I have no idea how pronounced this effect is.

 

[RPC]

Perhaps it could be adjusted to some degree with sulfite changes or adjusting other ingredients.. I will experiment if necessary.

 

[koraks]

I don't recall exactly what PE said some time ago to me about HAS, but it came down to HAS being a very weak developer and its effect in that respect may be too small to notice against the much larger activity of CD4. I suspect this is indeed the case, but it can't hurt to test.

As to the sulfite: perhaps it's enough in the scenario of capped, full bottles and one shot use. Relying on experience with lith developers that use around 2g sulfite per liter, I'd guesstimate that it would be at a critically low level in C41 as well, but it may just work if oxygen is kept away with mechanical means (ie the full bottle/one shot scenario).

 

[Rudeofus]

Sulfite, if present in sufficient amounts, will convert some oxidized CD-4 into a sulfonate, pretty much similar to the HQ ===> Q ===> HQMS reaction. This CD-4 Sulfonate is a poor and foggy developer - that's why PPD+sulfite based B&W developers are quite poor and slow. HAS, on the other side, may act as secondary developer for CD-4, and it will do some development on its own in highly developed regions. AFAIK sulfite and HAS have very different properties in combination with CD-4 and developable silver halide. If one could easily be replaced with the other, Kodak would have certainly used the much cheaper sulfite.

If you scan your results anyway, or optically enlarge subject matter where exact colors across the density range is not that critical, it may well be worth looking into whether HAS is that important. It's just one ingredient among many, it's not more expensive, more dangerous or more difficult to get than the rest of them.

 

[alanrockwood]

I realize this is an old thread, but let me continue.

For a long time I have been wondering about diluting C-41 developer. I just found a copy of Kodak's document on using C-41 chemicals. (Someone here at photrio provided a link to the document.) From the data in that document I was able to make some calculations to project the results for diluted C-41 developer at a 50% dilution. After I did the calculations I found this thread, which is very relevant to my question and calculations. I also found another thread on the topic of C-41 developer dilution. Here is the link. https://www.photrio.com/forum/threads/diluted-c41-tested.175919/. I could only reply to one thread, so I am choosing the earlier one.

Let me start with the bottom line. According to my calculations if you do a 50% dilution of the standard C-41 developer (LORR version), and leave out both the starter and the part B of the developer it should produce negatives that are very close to negatives produced under standard C-41 conditions.

Based on my calculations (which I will explain in more detail below) here is what you would do. Mix LORR C-41 developer but omit part B of the developer. Dilute the developer to the normal working concentration. Do not add the developer starter solution. Dilute again with an equal part of water. (There is a subtlety regarding this dilution that I might discuss later in the post, or maybe not, but I don't think that subtlety is very important, so I will skip it, at least for now.)

What you have now is a developer at 50% of the normal working concentration, but it is missing both part B of the developer and the developer starter. Omitting those to solutions basically compensates for the fact that this developer is not a replenished developer.

Use the developer as if it were a normal replenished developer, i.e. at normal times and temperatures.

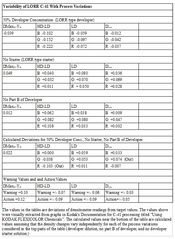
Based on my calculations here are the what the deviations in sensitometer readings would be compared to the target values

In the table above I retained all of the decimal places I used for the calculation, but you can round them off to two decimal places. Most of the values are within the specified ranges. Two of them are out of range, but only slightly out of range. The control limit for

I am attaching the files from which I took values for the calculation and the calculated results. The values were extracted visually from the graphs. I included three decimal points in the extracted data, which is probably within plus or minus 0.002 of the "true" values one would get from a perfect extraction of the values from the graphs.

With only two exceptions, all of the values are within control limits. The HD-LD parameter is -0.09, but the predicted value I get for this witches brew is -0.103 for the Red densitometer channel, which is out-of-control. However, this is so close that I doubt if anyone would be able to tell the difference in practice between an in-control process at an HD-LD of -0.09 and an out-of-control process at an HD-LD of -0.103. The green channel is out of control for Dmin, but only by +0.024, which again is close enough that I don't think it would make a difference that anyone would notice. (Note: Dmin is in the extreme shadow range.) And even if it did make a difference it is highly likely that any difference could be fixed by a very minor tweak in the curves in a scanned image or a very slight change in filtration in a darkroom-printed image.

I have not tried to verify these calculations using experimental measurements. There are a few limitations to this theoretical study. The first is the accuracy of Kodak's data. We just don't know how accurate the curves are.

The second limitation is the accuracy with which I extracted the numbers from the graphs. I already gave an estimate of what the precision is for the number-extraction process (probably plus or minus 0.002 units).

The most significant limitation is the underlying assumption made in the calculations, which is that the process variations affect the densities in an independent manner, so they can be combined by simply adding the variations together. For example, if the altered dilution gives a change in Dmin of value X, omitting part B of developer gives a change in Dmin of Y, and omitting the starter solution gives a change in Dmin of Z, then does the combination of process changes change the Dmin by X+Y+Z? Probably not, but I'll bet the assumption is probably at least roughly correct, and if that is true then the conclusion is valid that the altered C-41 process is good enough from all practical purposes.

Also to be considered is that this scheme is intended to be used with fresh solutions in a one-shot process, so any additional variability that can enter into the development process in a replenished system are eliminated, and that has to count for something.

Everyone is probably wondering about eliminating part B from the developer. Looking at the curves in the attached files it's pretty clear the part B mainly functions as a restrainer. Eliminating it is a major factor in bringing the activity of the dilute developer up to that of the developer at standard concentration.

Eliminating the starter is also a factor in bringing the performance of the diluted developer close to that of the developer under standard conditions.

Of course it's fair to ask whether anyone cares. Specifically, why would anyone want to run an altered C-41 process with diluted developer? I will leave that question for a separate discussion, but feel free to discuss the issue if you want.

 

[Rudeofus]

Very interesting work! Since I got confused initially by the term "calculated", I would like to get confirmation by you: "calculation" is basically adding up, what excessive dilution, lack of part B and lack of starter would yield, and balancing all these measures such that an optimal image would appear. Correct?

Did you just consider the end points of these graphs, or did you also try intermediate points (e.g. use only 10% of recommended starter)?

 

[alanrockwood]

Very interesting work! Since I got confused initially by the term "calculated", I would like to get confirmation by you: "calculation" is basically adding up, what excessive dilution, lack of part B and lack of starter would yield, and balancing all these measures such that an optimal image would appear. Correct?

Did you just consider the end points of these graphs, or did you also try intermediate points (e.g. use only 10% of recommended starter)?

You are correct. I simply added the three curves at their end points on the left-hand sides of the graphs.

I did not try any intermediate points. I considered calculating the results for some of the intermediate points but decided against it for various reasons, one of which is that it would have been a lot more work. Another is that it would make an additional (though slight) complication when preparing the solutions because the proposed scheme uses fewer solutions, omitting the addition of two solutions. Then there is the almost but not quite trivial issue that preparing solutions based on intermediate points would be a little more expensive.

All of that said, it would be interesting to do one intermediate condition, that condition being halfway between the points at the left had side of the graphs and the standard conditions.

I should probably re-emphasize that this is a paper study that has not been experimentally verified. Particularly important is whether the variables act independently or there are interactions between the variables that would invalidate simple addition of the density variations. However, is is encouraging that David Lyga seems to be getting good results under far greater dilution than my proposal.