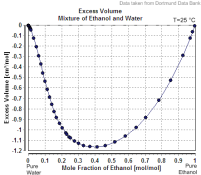
Doremus, dilutions usually do not follow total porportionality, errors that can be there may vary, this is the excess volume (deficit in this case) graph for water + ethanol
View attachment 249351
If you mix
1L of Ethanol 90%
+
1L of Ethanol 10%
then you won't get 2L , and it may not be Ethanol 50%, so not 50ml of pure ethanol in 100ml solution.
For this reason when an active substance is diluted in an "excipient" we use topping off, in that way we overcome the variable excess/deficit volume of mixtures that may be present, so we get accurate doses and exact calculations. You know, most darkroom mixtures use topping off.
Still, as Tom pointed, many times we may get well tolerable deviations for what's photography... But sometimes a pitfall can be there.