Film speed test in winter

[Chuck_P]

So, am I wrong in thinking that flare is a generalized, like pre-flashing.

Well, I don't think so. I like to equate it to pre-exposure to film, however---but I generalize it completely, perhaps even marginalize it, but I don't totally dismiss it. IMO, aparently, there's volumes that can be discussed in the theory, but it's relegated to much less discussion when it comes to actually photographing. That's not a jab at the discussion, it's just how I feel about it.

 

[Stephen Benskin]

Henry's book shows the effects of flare on the film's characteristic curve. This has long been the standard approach (up until computers became common); however, it doesn't represent how flare really works. It's a construct for the sake of simplification and easier than drawing a separate flare / camera image curve.



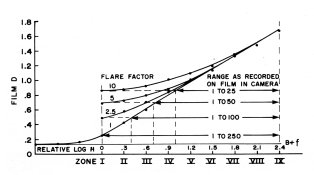
The one thing this type of graph does very effectively show is the reduced gradient caused by flare. Still, my belief is that the film's characteristic curve is a graphic depiction of how the film responds to exposure under specified processing conditions. An exposure of a given log-H will always fall at the same point on the curve. What the Henry curve does is to take what the density would be at Zone II 1/2 and places it on Zone I. But what really happens is flare moves the Zone I exposure to the right along the X-axis and it becomes the exposure where Zone II 1/2 would be in a non-flare situation.



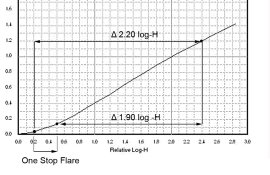
The above graph is how one stop of flare works. The shape of the film curve doesn't change, the optical image is what has changed in relation to the original image. This is why it's important to have no flare testing (if curve plotting is involved). As flare has little effect on the higher exposure values, the placement of the highlight exposure doesn't move. With the shift in the placement of the shadow exposure, the effective scene luminance range has shortened by one stop from a range of 2.20 to 1.90 (statistically normal flare is generally calculated at 0.34 to 0.40 reducing the illuminance range to 1.86 to 1.80). Normal processing would then be for a 6 1/3 stop range and not the original scene's 7 1/3 stop range.

The reason why most people don't have to worry about film with exposure is because it is built in (and as explained in the last paragraph). Without the effects of flare, the shadow exposure would fall approximately one stop further to the left. Flare moves the shadow exposure back up. The ISO film speed standard tests under no flare conditions, but factors in flare. For a 125 speed film, log-H at speed point should equal 0.0064 lxs.



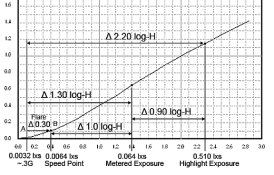
Published processing times also have flare factored in. Kodak's normal CI is 0.58. A statistically average scene has a luminance range of 2.20. The average grade 2 LER aim for a diffusion enlarger is 1.05. Based on the rise over run equation, these two stats would produce a CI of 0.48. If flare reduces the apparent luminance range by 0.40 making it 1.80, the resulting CI would be 0.58. So if you follow the instructions, you don't need to worry about normal flare.

Now the amount of flare tends to change with changes in luminance range. How this is handled can require some attention, but other factors can contribute to make any extra effort unnecessary. I like to keep the following graph in mind.



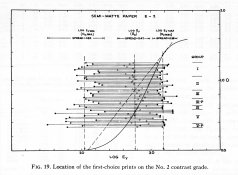
This shows the density ranges of negatives, that were judged to produce prints with excellent print quality, superimposed over the paper curve which they were printed on. Notice the diversity of NDRs. They all produced great prints. How precise does anyone actually have to be? Could this be the reason why good images are made regardless of the approach? The way I see it. Aim for the center. Even with all the potential variables and variances, you'll still hit the target.

 

[Bill Burk]

You guys are running away leaving me behind.
What I gather rather expose more to reduce flair instead of decreasing exposure. Which I think is better anyway if the light permits.
Otherwise if one decreases exposure one should extend development by an "X" amount to have a general compensation for the resulting flatness.
You do some disagree?

Hey AndreasT,

It's OK... High flare situations are not going to be flat so you don't extend development. There will be bright lights and dark shadows.

Old rule of thumb for amateurs is to expose more in high flare situations like backlighting and silhouette. That's only because of bad metering.

ChuckP is talking about metering carefully and then, because the shadows aren't as black as he wants, making them a little blacker.

 

[markbarendt]

You guys are running away leaving me behind.

You are not alone.

 

[markbarendt]

I like to equate it to pre-exposure to film,

And that is what I was trying to equate it to. Trying to use a concept that I think or at least thought I understood to understand the affect of veiling flare. By saying generalized, which is probably a bad choice of word, I meant to say flare affects the film all over or at least in areas where it is not intended to affect, much like pre-exposure does.

Pre-exposure, as I understand the concept, allows us to bring more shadow detail up into our printable range without increasing or affecting the rest of our image significantly, the higher values remain essentially pegged, they don't slide up the curve significantly. Pre-exposure allows us to minimize the image exposure to protect highlight separation. The only way I know to get a wider SBR to print straight onto a given grade of paper is by reducing the film's CI somewhere. Pre-exposure as I understand it, reduces the contrast in the shadows/flattens the toe to do this. This is what Dunn & Wakefield and Adams seem to be saying.

Is that understanding of pre-exposure true or false?

 

[Stephen Benskin]

Mark, you've got it. Pre-exposure is essentially the same as flare, effective film speed is increased and overall contrast reduced.

 

[Chuck_P]

That's it Mark, what Stephen said.

 

[AndreasT]

If flare / pre-exposure raises density more on the low density areas, then surely the density leat of the speed point would be raised more than the speed point resulting in less speed. No, Yes??

 

[Stephen Benskin]

If flare / pre-exposure raises density more on the low density areas, then surely the density leat of the speed point would be raised more than the speed point resulting in less speed. No, Yes??

No. Increased exposure in the shadow increases the shadow density and the speed point is reached with less exposure. This equals more speed.

 

[markbarendt]

Michael, I don't think it is actually less exposure in the shadows, especially with pre-exposure. It's pre-exposure + main exposure = normal shadow point. At the high end though total exposure can be lower.

With flare there is only one exposure so I'm not sure how that gets any extra.

 

[Stephen Benskin]

So I'll ask again - what is the purpose of giving less exposure? You might have a shorter print exposure time, but reduced local contrast in the shadow values in the negative - not a good thing from a Zone System perspective.

Why not just print through any density created by excessive flare.

So I actually disagree with the notion effective speed is increased by flare effects. Perhaps the speed "point" is increased, but local contrast in the shadows is decreased. If speed is a means to an end (ie sufficient local contrast in the shadows), we've lost more than we've gained, and this is compounded by reducing exposure.

There's flare and there's excessive flare. All optical systems have flare. We just don't notice it unless it's excessive. Normal shooting conditions have normal flare and flare is part of normal film processing and part of film speed.

Fun fact about flare and shadow compression. Ever wonder why Tri-X professional, with it's long toe, is considered a "studio" film? There's less flare with interiors and the ability to control lighting. In theory, regular Tri-X shot in daylight would have similar tonal distribution in the toe as Tri-X Pro shot in the studio.

 

[Bill Burk]

I'm just challenging the notion giving less exposure than one normally would, improves anything. If anything it puts more of the subject into the part of the curve that is compressed.

Now here is where I want to point out that you both can be right, and keep plugging away at what you like.

Michael R 1974, I am in the camp where I don't change EI based on conditions. So for simplicity, I would NOT lower my exposure when faced with a scene that is buzzing with flare.

CPorter, I totally support your idea to reduce exposure slightly in such a scene. Maybe you are holding your highlights off the shoulder? Maybe you see the shadows are badly compressed anyway so you aren't making things (much) worse than they already are.

But after staring at this flare-included camera step wedge test family of curves (thanks Rafal Lukawiecki for the data), I think Michael R 1974 is right. You are well-advised to get up out of the very flat toe. I would keep Zone I above the little diamonds (0.1 speed point) or at least above the little 'c' marks (they happen to be what I used as Contrast Index measurement endpoints, meaningless on their own, especially meaningless because of the flare, but I have a hunch these little 'c' marks are a good place for Zone I exposures).

 

[markbarendt]

I'm just challenging the notion giving less exposure than one normally would, improves anything. If anything it puts more of the subject into the part of the curve that is compressed.

My scientific wild ass guess is that in a situation where there is a bunch of flare in a given shot for whatever reason, there is a sweet spot somewhere; but we are between a rock and a hard spot.

On one side we have the toe that will compress important tones if we let placement fall too low, on the other when we add exposure excessive flare adds more and more generalized exposure that flattens the toe and reduces the the overall contrast of the image especially in the low tones.

For me, given my metering and shooting techniques, I normally have enough latitude to reduce my exposure by a stop in almost any situation without losing important detail. In a high flare situation I could give that latitude away to get better overall contrast. I peg my shots to the middle somewhere and very much live by what Stephan expresses here.

View attachment 63292

This shows the density ranges of negatives, that were judged to produce prints with excellent print quality, superimposed over the paper curve which they were printed on. Notice the diversity of NDRs. They all produced great prints. How precise does anyone actually have to be? Could this be the reason why good images are made regardless of the approach? The way I see it. Aim for the center. Even with all the potential variables and variances, you'll still hit the target.

Your system may not have the same latitude. That's not a detriment, it just means that you may already be at the sweet spot I might move to, to minimize flare.

 

[AndreasT]

No. Increased exposure in the shadow increases the shadow density and the speed point is reached with less exposure. This equals more speed.

Sorry I have to get back to this, if the shadows are more flat beacause of a pre-exposure the rise in the film is more gentle and surely you would have to travel more down the curve to the right to reach the speed point.
You have more density and theoretical speed increase over the unexposed film where there is no additional light.
Now if you want soft shadows like mentioned before thats fine but if I want to keep the contrast in the shadows I would have to eventually expose more.

 

[Chuck_P]

I've never reduced exposure more than 2/3 of a stop in an effort to counteract flare density in the low zones (nothing earth shattering), the notion that it causes problems is simply not realized in my experience. The very few times I have done it, only necessitated a quick re-evaluation of the important high value and planned developmet time.

Stephen points out that flare is always present to some degree, I simply do print through it as suggested, it's precisely why I rarely have ever made any attempt at compensation for it. But in the case of "excessive" flare possibilities, I have reduced exposure to no apparent problems----I would rather have a negative that minimizes it to some degree (which I believe that it does), while also printing through what remians. So, if after the shadow placement is made, it is believed that there is added density to it due to flare, then reduce exposure slightly to counteract it, re-evaluate the important high value, maybe adjust the planned development time, maybe not, make the exposure and move on. Some point of theory may suggest that this is detrimental, but I have some instances of photographing that suggests it is not.

Anyway, good or bad, that' how I do it, off to work now.
Chuck

 

[Stephen Benskin]

Also, let's not forget the loss of local contrast and reduced log-H range can be compensated by printing on a higher grade of paper. The increased slope of the higher grade of paper should help restore the local shadow contrast to a pleasing level.

 

[Stephen Benskin]

Sorry I have to get back to this, if the shadows are more flat beacause of a pre-exposure the rise in the film is more gentle and surely you would have to travel more down the curve to the right to reach the speed point.
You have more density and theoretical speed increase over the unexposed film where there is no additional light.
Now if you want soft shadows like mentioned before thats fine but if I want to keep the contrast in the shadows I would have to eventually expose more.

There's a difference between film speed and EI or personal taste. Different interpretation of terms plays a major roll in much of the miscommunication on these threads.

The ISO film speed standard incorporates a stop flare into the equation. The contrast parameters for development is to make the fixed density method correspond to the results from the fractional gradient method which bases speed on the shadow gradient. So gradient is a factor with ISO film speed. I'm not really sure what effect additional flare would have on the ratio between the fractional gradient point and the fixed density point of 0.10. Increased processing will reduce the ratio, which is why the fractional gradient method and Delta-X Criterion have effective film speeds that tend not to move with increased processing (a likely action with excessive flare).

 

[Stephen Benskin]

There's another factor that hasn't been address and that is the perception of the scene. The viewer expects a certain look from a backlit scene and that usually includes a flattening of the shadows. If the object of the photograph is to be natural looking, then snappy shadow contrast may not be appropriate. Personally, one of my favorate photographic approaches is to play against these kind of conventions.

 

[markbarendt]

There's another factor that hasn't been address and that is the perception of the scene. The viewer expects a certain look from a backlit scene and that usually includes a flattening of the shadows. If the object of the photograph is to be natural looking, then snappy shadow contrast may not be appropriate. Personally, one of my favorate photographic approaches is to play against these kind of conventions.

Yep.

There are also the considerations of imparting mood. The compression in the low end can impart an old time look or a boudoir look or in color photography a pastel look....

 

[Thomas Bertilsson]

Fun fact about flare and shadow compression. Ever wonder why Tri-X professional, with it's long toe, is considered a "studio" film? There's less flare with interiors and the ability to control lighting. In theory, regular Tri-X shot in daylight would have similar tonal distribution in the toe as Tri-X Pro shot in the studio.

A friend of mine pointed out something interesting that is practical application of this. Normally shooting portraits using Tri-X and HC-110, and switching to TMax 400 and Xtol, all of a sudden shadows were problematic due to flare. Solution? Expose TMax 400 at 1,000 to 1,200 and Xtol is still efficient enough in the shadows to get enough shadow detail - all while burying most of the flare. In fact, it looks a whole hell of a lot like Tri-X this way, and the advantage is of course that it gets easier to shoot medium format or large format with almost two extra stops of light. Just an aside, but it's a practical example of what you're saying.

 

[AndreasT]

The book of Henry is worth a read, what would it bring me?

 

[Stephen Benskin]

Michael, could you make my points from here on out? You do it so much better.

 

[Stephen Benskin]

It's sincerely meant to be a compliment. I wish I could make my points as well.

 

[AndreasT]

I thank you all for your thoughts and I will be reading more of all your stuff.
One thing I have noticed over the years having read many books, from Feininger, Adams, Barnbaum, Ctein, Lambrecht, Davis to name the more well known is that a lot contradict each other.
Many books just seem to copy what others have written in the past(not really meaning those mentioned above).
This is all very confusing, especially for people starting out. I worked until recently in a professional darkroom and there I have enlarged many negatives which were in an awful state exposure and development wise.
Not enought attention is given in my opinion to an important factor in the photography regarding exposure firstly and to a lesser degree development.
Too much attention is given to cameras, special magical developers etc. The handcraft needed for exposure is negleted too much.
Although for a few "mistakes" running in the wild out there I think aren't that bad since some of the information gets in a general good direction and should help even if not 100% correct.

This has also taught me to be sceptical and that led me to testing. I just hate reading long articles on the computer, it makes me giddy and nervous. I suppose I will print out a few things.

 

[Bill Burk]

Is that sarcasm again? If not, I've only repeated what you've said. And no matter how well anyone presents these points, in the end these exposure threads are pretty much the only place this sort of thing can be discussed. Over in the Film/paper/chemistry and Enlarging forums when anyone raises these issues they get hammered. It has happened to me many times.

Yes, It's sincere, Michael R 1974. You are really making clear posts that make sense.