The difference might be that I judge the intersection point(s) after applying a best-fit curve through the data points. Best-fit equations for s-shaped curves are not trivial.
The graphs aren't curve fits, but point-to-point graphs of the average of 3 independent runs. The run-to-run deviations were not large, the reason for the multiplicity was to remove the fliers one gets from operator error, defects in the paper, deviations in surface finish, etc. etc.
I did my master's in curve fitting algorithms and controls for NC machinery. Got a bookcase full of algorithms.
There is no reasonable way to fit VC paper to a curve - the stuff has 3 emulsions so you would need a summation of 3 emulsion curves. Most graded papers seem to be two emulsion VC-like papers - you can see the transition where the first emulsion shoulders out - so even there the situation gets complicated.
I found a power law fit works reasonably well, but the shoulder part of the curve is a bit of a problem. The physics behind the toe, 'linear' and shoulder regions are all different and if you use a function that is the same form as the underlying physics you end up with 3 functions for each emulsion.
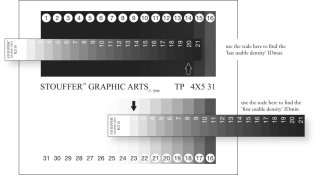
In any case there is no gain in 'smoothing' the data. The deviation from the true curve, whatever it is, to the linear approximation is less than the within-run print to print variation. There is even quite a bit of variation across a sheet of photographic paper. For precision work I find I need to take a serpentine path across the paper to minimize the distance from patch to patch. You can see this in the difference between the densities produced by the two #16 patches on a 31 step tablet.
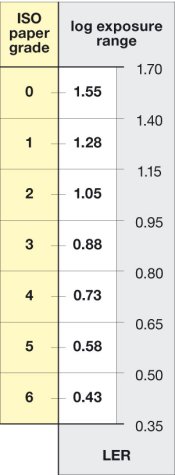
The manufacturer's data is very prettyfied, has no meaningful scale and is close to useless, though the Ilford curves at least do give an indication of the flat spot in the 00 curve.
The curves supplied on the web site can be trusted. I can read the light on the easel, go to the curve to find the exposure, expose, develop and dry and the density of the resulting print is what the curve indicates it should be.
What is very interesting isn't the HD curve but the derivative of the HD curve - a plot of local contrast. This really reveals the differences between papers and helps in picking the paper that has the right contrast in the right places.
If the equipment used assumes an ideal HD curve then there is no doubt you are going to be doing test strips... Even using the real curves still results in a need for test strips for some prints.
If you don't like ugly curves, then like most of reality, it is best not to look too close.