Kirk Keyes
Member
Sorry to all concerned if this thread brings up sad memories of another recent thread, but there was a big conceptual issue in that thread that went unresolved. As many of you know, I am big on finding analogies to help better our (my?) understanding of complicated concepts, and I thought of one that may have helped in that other thread. For some reason, that thread has been closed, so I am posting it here.
The opinion was stated several times in the other thread that a sheet of blank film cannot have a CI. In defending this opinion, it was said that the film must have at least two areas of exposure in order for the film to have recieved a development of a certain CI. I disagree with the opinion - CI is not dependant on exposure, and therefore a blank sheet can and will have whatever CI (or gradient or gamma or...) that it was processed to.
Here's my proof:
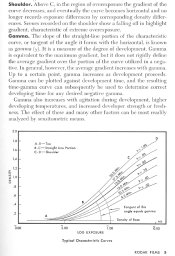
So let's take a sheet of film that has been exposed by contact printing it with a step tablet. Sufficient exposure was given to create a suitable range of film densities that will allow us to measure and calculate a CI. Let's say it has a CI of 0.60, just to give it a value.
I hope everyone will agree that this sheet, has a CI of 0.60 - we determined this by making measurements of all the wedge steps that were exposed onto the precessed film.
OK - and I think we will all agree that this sheet - the entire sheet of film - has a CI of 0.60. So now let's get our scissors out, and start cutting this sheet of film into smaller pieces. Let's cut it in half. We all agree that both halfs of our film have a CI of 0.60 still - the act of cutting the film will not change the contrast index of that peice of film.
So let's make a few more cuts. Say we separate out a few of the steps, one has a density of say 1.50, and another one a density of 0.74, and a third has a density of say 0.31. All of these steps still have a CI of 0.60. Cutting the film does not change the CI of our film.
OK, so now, let's cut out that step that has not recieved sufficient exposure to have gained any density at all - it is at the base+fog level of density. It is a "blank" piece of film. I hope that no one will argue that this film has a CI of 0.00, because it does not - it cannot. It has the same CI as the rest of that sheet of film. And therefore a peice of film does not have to have at least two different exposures to have a CI. It does to actually measure the CI, and they need to be the right exposures, but a films CI is purely dependant on the processing conditions.
So lets take this info and extend it to a second sheet of the same film as the one we just exposed with the step wedge and processed. That first precessed sheet of film had a CI of 0.60, the entire sheet did. And in the same processing batch, we had also run this second sheet. If the first sheet that we processed had a CI of 0.60, then we can be pretty certain that the second sheet does as well. (At least to the extent of our ability to measure CI when we consider sheet to sheet variability and the experimental error of measurement.)
Now if we had made an identical exposure of a step wedge on this second sheet, we could actually verify that it did receive the proper development to achieve a CI of 0.60 by measureing it and doing the calculations. And it should be very close, if not identical (remember the experimental error of the density readings as well as sheet to sheet variations.) If we had not used a step wedge, but had given enough of a fogging exposure to create a density on the sheet of 1.00, that's fine - as this film still has a CI of 0.60. If we had given a much larger exposure, then the density may well be 1.8, that's fine as well, as the film still has a CI of 0.60. If we had given no exposure to this second sheet, all's still fine - it also is processed to a CI of 0.60. CI is dependant on development, and not exposure.
Think about all the people that do roll film zone testing. They are using a series of exposures, each on an individual frame. They process the roll, measure densities, and calculate a CI. I hope no one will argue that each frame on that roll has been processed to a CI of 0.00 - although that is actually what has been argued here. While you can't calculate the CI of that roll using just one frame, each frame has been processed to some CI and it can be measured.
Let's stick some more sheets or rolls of the same film in the development batch and process them simultaneously, say in a drum or tank. Each roll in that run will have the same CI. If we did not make a proper set of exposures on some of those films, we cannot determine the actual CI the run was processed to. But, thanks to the science of process control, we don't need to actually have prepared a set of exposures to make the measurement of CI on each and every run. (This of course assumes that you do have control of your processing!!)
So I hope you all can see, it is very easy to give no exposure to a peice of film and process it so some CI value.
And I think the issue that was being pointed out about Davis' phrase "SBR", is that it should probably called "Subject Illumination Range - SIR", as an incident meter can only measure the light that falls on it - the amount of illumination, not "brightness".
Kirk - www.keyesphoto.com
The opinion was stated several times in the other thread that a sheet of blank film cannot have a CI. In defending this opinion, it was said that the film must have at least two areas of exposure in order for the film to have recieved a development of a certain CI. I disagree with the opinion - CI is not dependant on exposure, and therefore a blank sheet can and will have whatever CI (or gradient or gamma or...) that it was processed to.
Here's my proof:
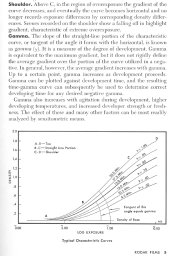
So let's take a sheet of film that has been exposed by contact printing it with a step tablet. Sufficient exposure was given to create a suitable range of film densities that will allow us to measure and calculate a CI. Let's say it has a CI of 0.60, just to give it a value.
I hope everyone will agree that this sheet, has a CI of 0.60 - we determined this by making measurements of all the wedge steps that were exposed onto the precessed film.
OK - and I think we will all agree that this sheet - the entire sheet of film - has a CI of 0.60. So now let's get our scissors out, and start cutting this sheet of film into smaller pieces. Let's cut it in half. We all agree that both halfs of our film have a CI of 0.60 still - the act of cutting the film will not change the contrast index of that peice of film.
So let's make a few more cuts. Say we separate out a few of the steps, one has a density of say 1.50, and another one a density of 0.74, and a third has a density of say 0.31. All of these steps still have a CI of 0.60. Cutting the film does not change the CI of our film.
OK, so now, let's cut out that step that has not recieved sufficient exposure to have gained any density at all - it is at the base+fog level of density. It is a "blank" piece of film. I hope that no one will argue that this film has a CI of 0.00, because it does not - it cannot. It has the same CI as the rest of that sheet of film. And therefore a peice of film does not have to have at least two different exposures to have a CI. It does to actually measure the CI, and they need to be the right exposures, but a films CI is purely dependant on the processing conditions.
So lets take this info and extend it to a second sheet of the same film as the one we just exposed with the step wedge and processed. That first precessed sheet of film had a CI of 0.60, the entire sheet did. And in the same processing batch, we had also run this second sheet. If the first sheet that we processed had a CI of 0.60, then we can be pretty certain that the second sheet does as well. (At least to the extent of our ability to measure CI when we consider sheet to sheet variability and the experimental error of measurement.)
Now if we had made an identical exposure of a step wedge on this second sheet, we could actually verify that it did receive the proper development to achieve a CI of 0.60 by measureing it and doing the calculations. And it should be very close, if not identical (remember the experimental error of the density readings as well as sheet to sheet variations.) If we had not used a step wedge, but had given enough of a fogging exposure to create a density on the sheet of 1.00, that's fine - as this film still has a CI of 0.60. If we had given a much larger exposure, then the density may well be 1.8, that's fine as well, as the film still has a CI of 0.60. If we had given no exposure to this second sheet, all's still fine - it also is processed to a CI of 0.60. CI is dependant on development, and not exposure.
Think about all the people that do roll film zone testing. They are using a series of exposures, each on an individual frame. They process the roll, measure densities, and calculate a CI. I hope no one will argue that each frame on that roll has been processed to a CI of 0.00 - although that is actually what has been argued here. While you can't calculate the CI of that roll using just one frame, each frame has been processed to some CI and it can be measured.
Let's stick some more sheets or rolls of the same film in the development batch and process them simultaneously, say in a drum or tank. Each roll in that run will have the same CI. If we did not make a proper set of exposures on some of those films, we cannot determine the actual CI the run was processed to. But, thanks to the science of process control, we don't need to actually have prepared a set of exposures to make the measurement of CI on each and every run. (This of course assumes that you do have control of your processing!!)
So I hope you all can see, it is very easy to give no exposure to a peice of film and process it so some CI value.
And I think the issue that was being pointed out about Davis' phrase "SBR", is that it should probably called "Subject Illumination Range - SIR", as an incident meter can only measure the light that falls on it - the amount of illumination, not "brightness".
Kirk - www.keyesphoto.com