I never used % reflectances to do anything anyway, but out of curiosity, where did the 18% myth come from then? And why does/did even Kodak sell "18% grey" cards?
Reflectance does come in handy with exposure models like for my program. Well not so much Reflectance but reflection density which is really just log(1/Reflectance). Just playing with some values and a few equations can really make clear how everything fits together.
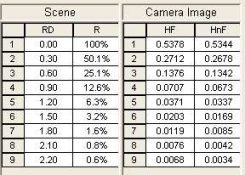

You can find more on this with a fairly detailed series of uploads titled Defining K: (there was a url link here which no longer exists)
I'm not sure if anyone has the answer to the origin of 18% gray. All I can offer is mostly speculation.
First of all, we're dealing with three different concepts. One is the perception of middle gray, the other is the average reflectance, and third is what the exposure meter uses.
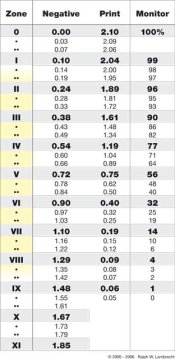
The first use of 18% that I know of comes from Munsell. He found that in a 10 step gray scale with visually equal steps, 18% fell in the middle on step 5 (remind anyone of something?). Jones heading JOSA's committee on Colorometry later adjusted this value to 19.6 (I think). So, one use of 18% is psychophysical. It's a good reference card.
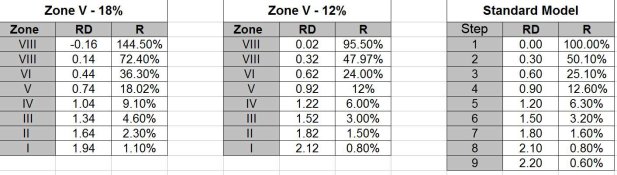
The second form of middle gray is from the average range of a scene. The statistically average scene has an luminance range of 2.20 logs or 7 1/3 from 100% R (0.0 RD) to 0.6% R (2.20 RD). The middle is 2.20/2 = 1.10 or 8%. If you round the scene to 7 stops, then the middle is 9%. This conforms with Jack Dunn's
Exposure Manual. This can be thought of as the middle gray for the physical scene.
The camera's middle gray is slightly different. Flare reduces the range to by ~ 0.34 or 1 1/4 stops (for a large format lens) to around 1.86. 1.86/2 = 0.93 or 11.7% which can be rounded to 12%. So, 12% can be considered the camera's middle gray.
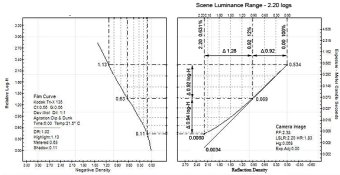
With the older uncoated lenses, flare was considered to be 2 stops. This makes the camera middle gray closer to 16%.
The final middle is exposure meters. A really quick way to determine what the Reflectance needs to be to produce the same results with a reflection meter as from an incident light meter, simply divide their constants. K for a reflection meter is 1.16. C for an incident meter is 30. 1.16* pi / 30 = 0.12
I'll have to check into it some, but the relationship between the two constants were different in the earlier standards. The problem is I don't think they had the hemisphere for incident meters when the first standards were developed in the mid 1940s, so I believe the value for C was for a flat plate receptor. I believe with this combination, something around 18% is possible.
I'm looking at the ISO 1994 standard,
General Purpose Photographic Exposure Meters (Photoelectric Type) - Guide to Product Specification. For the incident constant C, it has two types listed: Cardioid and Cosine. The cardioid (hemispherical) comes with the C = 30 and the cosine(flat plate) comes with a C around 20.3. For the same reflected exposure meter with a K = 1.16, the "reflectance" with the cardioid equals 12% and the reflectance with the cosine equals close to 18%. But this is mostly relative as exposure meters read luminance and not reflectance. The percentage comes from the calibration luminance of the reflection meter compared to the calibration illuminance of the incident meter.
Has anyone has read the exposure instructions that comes with the Kodak card? It says to open up 1/2 stop when metering the card in an exterior scene and not to adjust the exposure for an interior. In film school we were taught to meter exterior scenes with the dome and interior scenes with the flat plate. Notice how that corresponds to the hemispherical and flat plate receptors with the incident meters?
It's mostly speculative.