can I linearise this curve?

[percepts]

here's a question for the mathematicians amongst you all.

I have taken some measurements (using an EM10) which are:

21,24,29,38,53,72

the unit of change between each measurement is 1 (actually 1 stop of light less for each measurement. i.e. half the brightness each time).

the measuring device is obviously not linear in its response. Is there a way to calculate a formula to apply to measuremnts which results in a linear curve(straight)? The curve currently produced seems quite smooth so I thought it may be possible to calculate some formula from the result set I already have but I don't know how to do that.

thanks for any input.

 

[Shawn H]

Suppose you work out a fomula to do that. Then you'll have to run tests to confirm your formula. By the time that is done you might just as well use the experimental data anyway. How many stops of measurement do you need anyway?? 3~4 stops at the most, Right??

Shawn

 

[Photo Engineer]

I can tell you that a standard curve of Density vs Log E is called a cubic spline. If it fits that equation, then it fits a sensitometric curve. That assumes that each point on the x axis is represented by a real measurable change in Log E.

PE

 

[percepts]

Suppose you work out a fomula to do that. Then you'll have to run tests to confirm your formula. By the time that is done you might just as well use the experimental data anyway. How many stops of measurement do you need anyway?? 3~4 stops at the most, Right??

Shawn

if the formula is correct the result will be a straight line. The straightness of the line proves the formula as being correct. There is no need of testing other than charting the results to see if line is straight.

 

[Photo Engineer]

But that is the point. Some parts of the photographic response are not linear and cannot be mapped into a straight line. It depends on exposure and film or paper.

Good luck.

PE

 

[percepts]

But that is the point. Some parts of the photographic response are not linear and cannot be mapped into a straight line. It depends on exposure and film or paper.

Good luck.

PE

That is NOT the point. What has it to do with my question? I aksed about an EM10 which is a simple light measuring device and light was altered via enlarging lens stops. Paper and film simply don't come into this equation.

 

[Murray@uptowngallery]

linearization

I don't know it I'll be any help here.

I wasn't familiar with the instrument you referenced, but that's not important.

Non-linear data can be made to 'look' linear by plotting it on the appropriate scale.

If you take sets of numbers like the numbers 1-10 and the base-10 logarithm of each of those numbers and plot them on linear graph paper you get a noin-linear graph paper, you get a non-linear graph. If you plot them on, um, probably semi-logarithmic paper (linear on one axis, logarithmic on another), you get a straight line. You haven't changed the non-linear relationship between the numbers and the 'output' of the logarithmic function. You've only changed you way of looking at it.

f-stops and EV are scales or units to effectively linearize a range of light over a wide range, for convenience or usability. Very old meters just used an absolute measurement of foot candles or some other scaled unit, but that didn't immediately indicate what setings to use on a camera.

I didn't want to interpret what numbers should have been plotted against the ones you gave. To see their linearity or non-linearity one needs to see the pair of numbers making up each point (input and output).

I know there is an implied exponential or logarithmic (or both) relationship in measurements utilizing f-stops, but would have been second-guessing the actual raw numbers.

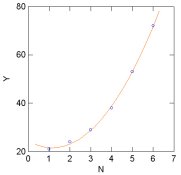
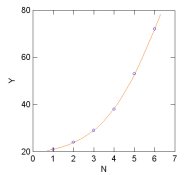
I made up some data pairs using your numbers just to see how they'd look with curve fitting (I use Curve Expert).

1) I simply numbered the data: (1,21),(2,24),(3,29),(4,38),(5,53),(6,72)
2) I used an exponential spacing analogous to f-stops, 1, 1.414, 2, 2.828, etc
3) I used powers of 2 (1, 2, 4,8,16, 32)

I don't understand why I almost always get best results with polynomial curve fits, even where the data has a logarithmic function, but that's what happened. Using a 4th-order polymnomial, it gave the best results.

What you could do with this is end up with a function that allowed you to recreate the curve that produces your data above and allows you to interpolate (read between the data points) over the range of data you've collected.

I don't know if this answers your question, but it points out why a previous respondent implied the question is a bit open ended, a bit ambiguous. You've already implied there is some ambiguity in the relationship between the points. I implied you can screw up the scaling to make it 'look' linear, but it probably isn't, at it's core.

I don't understand what kind of solution you need.

I think the sensor in the instrument is probably intentionally non-linear because it's a way of making a very wide range of data fit a practical range. That's the way it is in nature, measuring physical phenomena like light, sound etc.

If this helps you fine tune the question , maybe we can fine tune an answer.

If it's just to explore the phenomenon, that's fine. I do that alot, where other people use Sunny-16 and produce more images than me.

Do you see the point that the data may be linear or non-linear depending on the relationship of the units of input and output?

If you looked at a table of EV versus foot-candles or foot-lamberts (some spotmeters used to have such a table in the manual), the EV 'input' is linear and the output is not.

 

[Lee L]

... and light was altered via enlarging lens stops. Paper and film simply don't come into this equation.

Explaining this earlier would have made your question clearer. It's not unreasonable for Ron to have assumed that you were using the meter for measuring differences in processed film with one stop differences in exposure. One reason I didn't consider working on an answer to your question when it first appeared was that your method and purpose were ambiguous. You might also get more accurate attenuation from a decent step wedge rather than your enlarging lens click stops.

I'm not much of a mathematician, but now that I know what you're up to, I'll give it some time when I can and respond if someone else doesn't beat me to it.

Lee

 

[dancqu]

I have taken some measurements (using an EM10) which are:
21,24,29,38,53,72
the unit of change between each measurement is ... half the
brightness each time).
...the measuring device is obviously not linear in its response.

That's right, the EM-10 is not linear. The best that can be
done in graphing is to plot f stop against number on the dial.
A chart of the two will tell just as much.

I've calibrated my EM-10 against a step wedge and can now
use it on easel as a transmission densitometer. Dan

 

[john_s]

Doing a chart in Excel and finding a trend line, gives the polynomial:
y = 2.1429x^2 - 4.9714x + 24.4
where y=measured value, x=number of measurement (first=1),
with R^2 = 0.9989 (which means good approximation)

If you want to interpolate intermediate values, I guess this would give good results.

 

[Photo Engineer]

Lee;

Thanks. That is exactly what I assumed since it was in the Enlarging forum and there was no other accompanying explanation.

The answers by Murray and John show the non-linear nature of the light quite well with rather straightforward methods.

Sorry for the misunderstanding.

PE

 

[Neil Poulsen]

I find a better fit for the data is the following:

Y = 18.061970 + 1/[ 0.008193 + 0.660672 * (0.5)^N ]

This takes advantage of the known fact that the amount of light for each measurement is half that of the previous measurement. In this case, N=1,2,3,4,5,6.

R-Square for this fit is R2 = 0.999984. That's very good for practical data.

What would be interesting to determine is the theoretical relationship between these two variables. I don't know much about what was measured, though. This model appears to approximate the actual relationship fairly closely.

The first graph shows the fit of the quadratic. The second graph shows a fit of this model.

After graphing the data, the quadratic is a decent choice and worth trying. But graphing the data against X=32,16,8,4,2,1 leads one to think that the relationship might be some sort of reciprical, which is what led to the choice of the above model.

 

[percepts]

Thanks all,

I now have a formula which is:

x = 1 ± √ (y/2 - 11)

which works providing y is ge 22

 

[greybeard]

It appears that what you have done is to map the transfer function between the aperture ring markings on your particular enlarger light source and lens, to the readout on the EM10. The f/ stop markings are not necessarily accurate, and there is also absorption in the lens, scatter, and the effects of ambient light (either from safelights or light leakage from the enlarger). It may be that you get exactly a factor of two in illumination between successive stops, or it may not.

For simple interpolation, this probably doesn't matter; if you are trying to do sensitometry, it probably does.

 

[johnnywalker]

If you want to play around with it yourself, go to:

http://www.ebicom.net/~dhyams/cmain.htm

and download the software (Curve Expert) to find the appropriate regression equation.

 

[percepts]

If you want to play around with it yourself, go to:

http://www.ebicom.net/~dhyams/cmain.htm

and download the software (Curve Expert) to find the appropriate regression equation.

now thats a very useful link. I have played and applied the cubic spline as suggested by PE and it seems to fit very well. But I now have a further question.

The cubic spline equation given by the software is :

y = ax³ + bx² + cx + d

so where or what are a b c and d and how do I rearrange the formula so that I have x = f

 

[Lee L]

The cubic spline equation given by the software is :

y = ax³ + bx² + cx + d

That's not a cubic spline, it's a polynomial (specifically a third order, or cubic polynomial), which can be calculated with the linest function (or equivalent) in any decent spreadsheet. For an explanation of the difference, see: http://online.redwoods.cc.ca.us/instruct/darnold/LAPROJ/Fall98/SkyMeg/splinepres/sld001.htm

Lee

P.S. I just downloaded and ran the curve expert program in linux under wine, and it works, but I can't see how or why it's getting cubic spline info. That's not one of the options under the "apply fit" menu, but is under "interpolate". When you do see the cubic spline fitted curve, you don't get any numbers to use in an equation, just NA for (I assume) "not applicable". What you do get is the numbers for the cubic polynomial equation. You'll have to get the author of the software to explain this.

The software does claim that the best fit is a 4th order polynomial, but I suspect that it's just trying to make allowance for some non-linear variable in your setup. I'd suspect some combination of inexact aperture markings and the non-proportional mix of stray light (bounced off the walls or your shirt or arm) with direct light from the projected image. The MMF model in Curve Expert actually appears to be a better description of the behavior to me.

 

[percepts]

That's not a cubic spline, it's a polynomial (specifically a third order, or cubic polynomial), which can be calculated with the linest function (or equivalent) in any decent spreadsheet. For an explanation of the difference, see: http://online.redwoods.cc.ca.us/instruct/darnold/LAPROJ/Fall98/SkyMeg/splinepres/sld001.htm

Lee

P.S. I just downloaded and ran the curve expert program in linux under wine, and it works, but I can't see how or why it's getting cubic spline info. That's not one of the options under the "apply fit" menu, but is under "interpolate". When you do see the cubic spline fitted curve, you don't get any numbers to use in an equation, just NA for (I assume) "not applicable". What you do get is the numbers for the cubic polynomial equation. You'll have to get the author of the software to explain this.

The software does claim that the best fit is a 4th order polynomial, but I suspect that it's just trying to make allowance for some non-linear variable in your setup. I'd suspect some combination of inexact aperture markings and the non-proportional mix of stray light (bounced off the walls or your shirt or arm) with direct light from the projected image. The MMF model in Curve Expert actually appears to be a better description of the behavior to me.

Well yes I thought it was cubic spline because thats what it said it was.
I have played some more and if you use the file/export you are given the abcd numbers. The reason, I think, they are not given by the graph is because they change between each two points on the curve which makes the formula no use to me. However, since I can generate a table of values for for given vlaues along the curve I can create a simple and accurate lookup chart for time factors between two readings which is where I was trying to get to. Problem solved.

Thanks all.

 

[Lee L]

The reason, I think, they are not given by the graph is because they change between each two points on the curve which makes the formula no use to me.

Yes, it's the piecewise nature of the cubic spline that means you don't get a list of the shifting coefficients in the Model Information window that displays when you click the Info button on the cubic spline interpolation graph. That's the reason you get Not Applicable rather than a list of coefficients (what you're calling abcd...). The list of 5 cubic polynomial expressions you're seeing in the export file are the ones you'd use between sequential data pairs.

I'd still be inclined to look outside the EM10 for at least one source of the "error" you're trying to quantify.

Lee

 

[Lee L]

OK, lemme take one last stab at this and then I'm bugging out for my kid's birthday weekend.

You expect a reciprocal relationship between exposure time and aperture. The traditional way to put time and aperture in a linear relationship is to use the standard base 10 log of the factors involved, so one stop = log10(2) = 0.30, two stops = log10(4) = 0.60, etc. You can also do this with your exposure times in seconds, in the case of your data set log10(21) = 1.3222, log10(24) = 1.3802, etc. Doing this converts your data set to:

0.00 1.3222
0.30 1.3802
0.60 1.4623
0.90 1.5707
etc.

You can do the base 10 log of your EM10 numbers in Curve Expert through the menu Data | Transform and choosing to apply log(x) to the Y column (assuming that's where your EM10 numbers are). Put the sequence for one stop of change in the X column as 0.00, 0.30, 0.60 ... adding one stop of 0.30 log density for each step.

Now run a regression in Curve Expert using the reciprocal model. You'll get the curve in the first attached image and equation and coefficients in the second attached image.

Now you've actually run the regression against log10 in Curve Expert, so you need account for that and then balance the equation to put y as the lone term on the left of the equation. Doing that gives you: y=10^(1/ax+b), where y is the expected readout from the EM10, a=-0.15260376, b=0.76729945, and x is expressed in standard log density terms with each stop equal to 0.3. This is the expected reciprocal relationship between time and f-stops and a very good match to the data. I'd suggest that trying to take your data as "perfect" and tweak the equations to match relatively small data errors is not going to provide any real gains. Try another set of 10 measurement runs, and check for differences due to the direction in which you approach the f-stops. Also, wear a black long sleeved shirt, kill all safelights, and eliminate all light leaks from the enlarger when you do this. My guess is that you'll find that measurement error swamps the fine tweaking you're trying to do with high order polynomials.

Then again, I could be completely wrong.

Lee

 

[percepts]

There was a much simpler way which is to swap axes so meter readings are on X and stops are on Y. But then you convert stops to time so that you have 1,2,4,8,16 etc and then you run a bicubic spline and set the graph properties to increments of 1 on both axes and what you get is the following:

note that I redid measurements to include the greatest brightness range I could get out of my enlarger.

To use lookup table, just make two readings with your EM10, divide the lower time into the higher time then multiply or divide your exposure time depending on which way you are moving. i.e. the result of the first divide is a print time factor.

<pre>
Reading Time from base of reading at 7.
7 1.00
8 1.48
9 2.00
10 2.58
11 3.24
12 4.00
13 4.87
14 5.83
15 6.88
16 8.00
17 9.19
18 10.50
19 12.02
20 13.83
21 16.00
22 18.64
23 22.00
24 26.36
25 32.00
26 39.06
27 47.12
28 55.62
29 64.00
30 71.82
31 79.06
32 85.82
33 92.20
34 98.30
35 104.21
36 110.04
37 115.88
38 121.84
39 128.00
40 134.45
41 141.17
42 148.13
43 155.29
44 162.61
45 170.06
46 177.59
47 185.18
48 192.79
49 200.38
50 207.91
51 215.35
52 222.66
53 229.80
54 236.74
55 243.45
56 249.88
57 256.00
58 261.81
59 267.49
60 273.24
61 279.28
62 285.81
63 293.06
64 301.22
65 310.51
66 321.14
67 333.33
68 347.27
69 363.19
70 381.30
71 401.80
72 424.91
73 450.84
74 479.80
75 512.00
76 547.56
77 586.26
78 627.79
79 671.82
80 718.06
81 766.17
82 815.85
83 866.79
84 918.67
85 971.18
86 1024.00
87 1076.82
88 1129.33
89 1181.21
90 1232.15
91 1281.83
92 1329.94
93 1376.18
94 1420.21
95 1461.74
96 1500.44
97 1536.00
98 1568.11
99 1596.46
100 1620.72
</pre>

at lower meter readings it won't be very accurate because of small change in metered reading for large change in brightness. Large meaning half a stop is not accurately measurable down at meter readings below approx 16. However, for most practical purposes you would never be using your enlarger that bright unless you were printing 6x4 with no filtration and no neutral density.

 

[Chan Tran]

I simply take the reciprocal of the readings and the plot look quite straight.