alanrockwood
Member
- Joined
- Oct 11, 2006
- Messages
- 2,185
- Format
- Multi Format
Is there any software out there that takes a sampled image (e.g. from a Bayer sensor or a Foveon sensor, or whatever) and applies a proper signal reconstruction filter to it to do the best possible reconstruction of the image?
It's easiest to talk about this in one dimension. It's well-known that a signal sampled at a rate higher than twice the frequency of the signal allows one to do an error-free reconstruction of the original signal. This implies that there can be no signal components above this critical frequency. If the signal is more than twice the sampling rate then you can't reconstruct the original signal without the benefit of some kind of additional information. What happens is that the sampled signal is aliased, that is it appears as if it were a lower frequency signal.
What is less known by the general public (though it is known to experts in signal processing) is that you can't just take the sampled signal as a good representation of the analog signal. If the signal frequency is relatively low compared to the sampling frequency this can work pretty well, but if the signal frequency is close to the Nyquist limit, though still within the Nyquist limit, then the sampled points cannot be taken directly as a good representation of the original signal. In fact, it looks very much like an aliased signal.
The key fact here is that, as mentioned above, you can't just take the sampled points as giving a good representation of the original analog signal. (Forgive me if I am repeating myself.) To do a proper reconstruction of the original signal you need to apply a reconstruction filter. An if you want to give a perfect reconstruction of the original signal the reconstructed signal must be a continuous function, i.e. not represented by a finite number of points. However, if you want to give an accurate reconstruction using a finite number of points you need to use more points than the number of points with which you sampled the original signal. I believe that as a rule of thumb you would need twice the number of points that were sampled, but don't quote me on that as being a rigorous result. However, for sake of discussion let's just assume that the suggested rule of thumb is correct. The analogous rule of thumb for a two dimensional signal, i.e. and image, would be four times as many points as the number of points you sampled.
This long introduction brings me to the question: Is there any software out there that applies a proper reconstruction filter to a sampled image? The output of the software would be a re-sampled function of four times as many points, assuming my rule of thumb is correct, but in any case, it will be some multiple of the originally sampled number of points. For example, a 10 megapixel image as it comes out of the camera might be reconstructed as a forty megapixel image.
Note, I am not trying to beat the Nyquist limit here. I am only trying to get the maximum amount of information available within the constraints of the Nyquist limit. This could allow the reconstruction of finer details than would be evident if we simply took the original sampling points as the image.
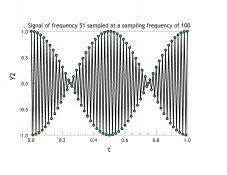
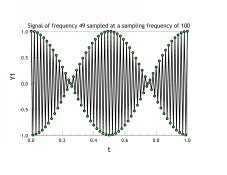
I am including an image of two signals sampled at sampling frequency of 100 (arbitrary units). In one figure the signal frequency is just barely within the Nyquist limit (frequency = 49 arbitrary units), and in the other figure the signal is just barely above the Nyquist limit (frequency = 51 arbitrary units). The two sampled signals are identical. The underlying signal is a simple cosine function, so the beat pattern you see tells us that the signal "reconstruction" is not error free. The reason is that we have taken the sampled points themselves as if they were the reconstruction rather than applying a proper reconstruction filter to the sampled results.
It's easiest to talk about this in one dimension. It's well-known that a signal sampled at a rate higher than twice the frequency of the signal allows one to do an error-free reconstruction of the original signal. This implies that there can be no signal components above this critical frequency. If the signal is more than twice the sampling rate then you can't reconstruct the original signal without the benefit of some kind of additional information. What happens is that the sampled signal is aliased, that is it appears as if it were a lower frequency signal.
What is less known by the general public (though it is known to experts in signal processing) is that you can't just take the sampled signal as a good representation of the analog signal. If the signal frequency is relatively low compared to the sampling frequency this can work pretty well, but if the signal frequency is close to the Nyquist limit, though still within the Nyquist limit, then the sampled points cannot be taken directly as a good representation of the original signal. In fact, it looks very much like an aliased signal.
The key fact here is that, as mentioned above, you can't just take the sampled points as giving a good representation of the original analog signal. (Forgive me if I am repeating myself.) To do a proper reconstruction of the original signal you need to apply a reconstruction filter. An if you want to give a perfect reconstruction of the original signal the reconstructed signal must be a continuous function, i.e. not represented by a finite number of points. However, if you want to give an accurate reconstruction using a finite number of points you need to use more points than the number of points with which you sampled the original signal. I believe that as a rule of thumb you would need twice the number of points that were sampled, but don't quote me on that as being a rigorous result. However, for sake of discussion let's just assume that the suggested rule of thumb is correct. The analogous rule of thumb for a two dimensional signal, i.e. and image, would be four times as many points as the number of points you sampled.
This long introduction brings me to the question: Is there any software out there that applies a proper reconstruction filter to a sampled image? The output of the software would be a re-sampled function of four times as many points, assuming my rule of thumb is correct, but in any case, it will be some multiple of the originally sampled number of points. For example, a 10 megapixel image as it comes out of the camera might be reconstructed as a forty megapixel image.
Note, I am not trying to beat the Nyquist limit here. I am only trying to get the maximum amount of information available within the constraints of the Nyquist limit. This could allow the reconstruction of finer details than would be evident if we simply took the original sampling points as the image.
I am including an image of two signals sampled at sampling frequency of 100 (arbitrary units). In one figure the signal frequency is just barely within the Nyquist limit (frequency = 49 arbitrary units), and in the other figure the signal is just barely above the Nyquist limit (frequency = 51 arbitrary units). The two sampled signals are identical. The underlying signal is a simple cosine function, so the beat pattern you see tells us that the signal "reconstruction" is not error free. The reason is that we have taken the sampled points themselves as if they were the reconstruction rather than applying a proper reconstruction filter to the sampled results.